题目内容
11. 如图,质量为m长为L的均匀细直杆竖直放置,杆下端与地面之间的摩擦系数为μ,杆上端用绳索拉住,绳子与直杆之间的夹角为θ,在离地面高度为h处以水平力F作用与直杆,试问使直杆不滑倒,作用力F的最大值应是多少?
如图,质量为m长为L的均匀细直杆竖直放置,杆下端与地面之间的摩擦系数为μ,杆上端用绳索拉住,绳子与直杆之间的夹角为θ,在离地面高度为h处以水平力F作用与直杆,试问使直杆不滑倒,作用力F的最大值应是多少?
分析 根据力矩平衡条件,结合受力平衡及矢量合成法则,并结合数学运算公式,即可求解.
解答 解:以杆和地面接触点为支点,根据力矩平衡:
Fh=TLsinθ
解得:T=$\frac{Fh}{Lsinθ}$
根据受力平衡,地面压力:N=Tcosθ+mg=Fhctgθ×$\frac{1}{L}$+mg
以杆和绳索接触点为支点,根据力矩平衡,得到地面摩擦力:
fL=F(L-h)
解得:f=$\frac{F(L-h)}{L}$
由f≤μN
可得:F$\frac{L-h}{L}$≤μ($\frac{Fhctgθ}{L}$+mg)
F≤$\frac{μmgL}{L-h-μhctgθ}$
当L-h-μctgθh≤0的时候,即h≥$\frac{L}{1+μctgθ}$时,
f≤μN恒成立,此时无论用多大的力F,杆都能保持平衡.
答:使直杆不滑倒,作用力F的最大值$\frac{μmgL}{L-h-μhctgθ}$,而当h≥$\frac{L}{1+μctgθ}$时,f≤μN恒成立,此时无论用多大的力F,杆都能保持平衡.
点评 考查受力平衡与力矩平衡的应用,掌握矢量合成法则的内容,注意h高度取值是解题的关键.

练习册系列答案
相关题目
19.下列电器中,不是应用了电磁感应现象的是( )
| A. | 交流发电机 | B. | 变压器 | ||
| C. | 白炽灯 | D. | 汽车防抱死制动系统(ABS) |
16.如图为沿同一直线运动的甲、乙两物体在0-t0时间内的s-t图象由图象可知( )
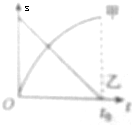

| A. | 甲、乙两物体沿相反方向运动 | |
| B. | 甲运动越来越慢,位移越来越小 | |
| C. | 0-t0时间内乙物体的位移为零 | |
| D. | 0-t0时间内两物体间的距离先变小后变大 |
2.把质量为m的正点电荷放在电场中无初速度释放,不计重力,则以下说法正确的是( )
| A. | 点电荷的轨迹一定和电场线重合 | |
| B. | 点电荷的速度方向总是与所在处的电场线方向一致 | |
| C. | 点电荷的加速度方向总是与它所在处的电场线的切线方向重合 | |
| D. | 点电荷将沿电场线切线方向抛出,做抛物线运动 |
3.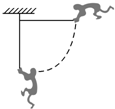 “神舟”七号宇航员在进行素质训练时,抓住秋千杆由水平状态开始下摆,如图所示,到达竖直状态的过程中,宇航员所受重力的瞬时功率变化情况是( )
“神舟”七号宇航员在进行素质训练时,抓住秋千杆由水平状态开始下摆,如图所示,到达竖直状态的过程中,宇航员所受重力的瞬时功率变化情况是( )
 “神舟”七号宇航员在进行素质训练时,抓住秋千杆由水平状态开始下摆,如图所示,到达竖直状态的过程中,宇航员所受重力的瞬时功率变化情况是( )
“神舟”七号宇航员在进行素质训练时,抓住秋千杆由水平状态开始下摆,如图所示,到达竖直状态的过程中,宇航员所受重力的瞬时功率变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
 如图所示,在磁感应强度为B=1T的匀强磁场中,有半径为l=0.2m的光滑半圆导体框架ab,OC为一根能绕O点在框架上转动的导体棒,导体棒电阻为r=0.2Ω,电阻R=0.8Ω,导体框架电阻不计,在OC以角速度ω=10rad/s绕O点匀速转动的过程中,求电阻R消耗的电功率?
如图所示,在磁感应强度为B=1T的匀强磁场中,有半径为l=0.2m的光滑半圆导体框架ab,OC为一根能绕O点在框架上转动的导体棒,导体棒电阻为r=0.2Ω,电阻R=0.8Ω,导体框架电阻不计,在OC以角速度ω=10rad/s绕O点匀速转动的过程中,求电阻R消耗的电功率? 某实验小组利用实验室提供的器材,探究一种横截面为圆形的金属丝的电阻率,他们使用千分尺测量金属丝的直径,示数如图所示,这种金属丝的直径为0.260mm.
某实验小组利用实验室提供的器材,探究一种横截面为圆形的金属丝的电阻率,他们使用千分尺测量金属丝的直径,示数如图所示,这种金属丝的直径为0.260mm.
