Question

【题目】如图所示，细绳的一端系着质量为M=2kg的物体，静止在水平圆盘上，另一端通过光滑的小孔吊着质量为m=0.5kg的物体，M的中点与圆孔的距离为0.5m，并已知M与圆盘的最大静摩擦力为4N，现使此圆盘绕中心轴线转动，求角速度ω在什么范围内可使m处于静止状态？（g取10m/s2）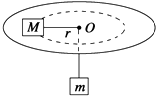

Answer 1

【答案】解：当ω取较小值ω1时，M有向O点滑动趋势，此时M所受静摩擦力背离圆心O，对M有：mg﹣Fmax=Mω 2r，
代入数据得：ω1=1 rad/s．
当ω取较大值ω2时，M有背离O点滑动趋势，此时M所受静摩擦力指向圆心O，对M有：
mg+Fmax=Mω22r
代入数据得：ω2=3 rad/s
所以角速度的取值范围是：1 rad/s≤ω≤3 rad/s．
答：角速度ω在1 rad/s≤ω≤3 rad/s的范围内可使m处于静止状态
【解析】当此平面绕中心轴线以角速度ω转动时，若M恰好要向里滑动时，ω取得最小值，此时M所受的静摩擦力达到最大，方向沿半径向外，由最大静摩擦力和绳子拉力的合力提供M所需要的向心力．若M恰好要向外滑动时，ω取得最大值，此时M所受的静摩擦力达到最大，方向沿半径向里，由最大静摩擦力和绳子拉力的合力提供M所需要的向心力．根据牛顿第二定律分别求出ω的最小值和最大值，即可得到ω的取值范围．
【考点精析】通过灵活运用向心力，掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力即可以解答此题．