题目内容
4.A、B两质点分别做匀速圆周运动,在相同时间内,它们通过的弧长之比SA:SB=2:3,而转过的角度之为ϕA:ϕB=3:2,则它们的周期之比TA:TB=2:3,半径之比RA:RB=4:9.分析 根据角速度和线速度的定义求解线速度与角速度之比,根据角速度与周期的关系求周期之比,再根据角速度与线速度的关系求半径之比.
解答 解:根据角速度的定义$ω=\frac{φ}{t}$知,在相等时间里,角速度大小之比等于转过的角度比,即:ωA:ωB=φA:φB=3:2
根据$T=\frac{2π}{ω}$,知$\frac{{T}_{A}}{{T}_{B}}=\frac{{ω}_{B}}{{ω}_{A}}=\frac{2}{3}$
根据线速度$v=\frac{s}{t}$知,在相等时间里,线速度大小之比等于通过的弧长之比即:vA:vB=sA:sB=2:3
又:v=ω•r,所以:$r=\frac{v}{ω}$,所以:$\frac{{r}_{A}}{{r}_{B}}=\frac{\frac{{v}_{A}}{{ω}_{A}}}{\frac{{v}_{B}}{{ω}_{B}}}=\frac{{v}_{A}}{{v}_{B}}•\frac{{ω}_{B}}{{ω}_{A}}=\frac{2}{3}•\frac{2}{3}=\frac{4}{9}$
故答案为:2:3,4:9
点评 该题考查圆周运动的过程中的线速度、角速度与周期的关系,熟练描述圆周运动物理量的定义及相互间关系是正确解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
15. 如图所示为实验室模拟远距离输电的实验电路图,两理想变压器的匝数比分别为n1:n2=1:10、n3:n4=10:1,两根模拟输电线的总电阻用R0表示,R0=5Ω.输入端A、B接入电压恒定的正弦交流电.若在C、D两端接入一个灯泡(额定功率10W,额定电压10V),灯泡恰能正常发光.下列说法正确的是( )
如图所示为实验室模拟远距离输电的实验电路图,两理想变压器的匝数比分别为n1:n2=1:10、n3:n4=10:1,两根模拟输电线的总电阻用R0表示,R0=5Ω.输入端A、B接入电压恒定的正弦交流电.若在C、D两端接入一个灯泡(额定功率10W,额定电压10V),灯泡恰能正常发光.下列说法正确的是( )
 如图所示为实验室模拟远距离输电的实验电路图,两理想变压器的匝数比分别为n1:n2=1:10、n3:n4=10:1,两根模拟输电线的总电阻用R0表示,R0=5Ω.输入端A、B接入电压恒定的正弦交流电.若在C、D两端接入一个灯泡(额定功率10W,额定电压10V),灯泡恰能正常发光.下列说法正确的是( )
如图所示为实验室模拟远距离输电的实验电路图,两理想变压器的匝数比分别为n1:n2=1:10、n3:n4=10:1,两根模拟输电线的总电阻用R0表示,R0=5Ω.输入端A、B接入电压恒定的正弦交流电.若在C、D两端接入一个灯泡(额定功率10W,额定电压10V),灯泡恰能正常发光.下列说法正确的是( )| A. | R0两端的电压为0.5V | |
| B. | A、B端的输入电压为10.5V | |
| C. | A、B端的输入功率为10.05W | |
| D. | A、B端输入电压变小,R0上损失的功率可能不变 |
13. 测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
 测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )
测定运动员体能的一种装置如图所示,运动员质量为m1,绳拴在腰间沿水平方向跨过一个轻质且不计摩擦的滑轮,悬挂重物m2,人用力蹬传送带而人的重心相对于地面不动,使传送带上侧以速率v向右运动,下面是关于人对传送带做功的说法,正确的是( )| A. | 人对传送带做负功 | B. | 人对传送带不做功 | ||
| C. | 人对传送带做功的功率为m2gv | D. | 人对传送带做功的 功率为(m1+m2)gv |
14.有人站在火车轨道旁,一列迎面高速驶来的火车正在鸣笛,则他听到的鸣声频率将比喇叭实际发出声音的频率( )
| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不能确定 |
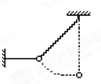 如图所示,一根轻弹簧和一根细绳共同拉住一个重物,平衡时细绳恰处水平,此时弹簧的弹力大小为80N,若烧断细绳,测出小球运动到悬点正下方时弹簧的长度正好等于未烧断细绳时弹簧的长度,试求:小球运动到悬点正下方时向心力的大小.
如图所示,一根轻弹簧和一根细绳共同拉住一个重物,平衡时细绳恰处水平,此时弹簧的弹力大小为80N,若烧断细绳,测出小球运动到悬点正下方时弹簧的长度正好等于未烧断细绳时弹簧的长度,试求:小球运动到悬点正下方时向心力的大小. 如图所示,质量为m=2kg的物块放在一固定斜面上,斜面长L=11m,当斜面倾角为37°时物块恰能沿斜面匀速下滑.现对物体施加一大小为F=100N的水平向右恒力,可使物体从斜面底端由静止开始向上滑行,求(已知sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,质量为m=2kg的物块放在一固定斜面上,斜面长L=11m,当斜面倾角为37°时物块恰能沿斜面匀速下滑.现对物体施加一大小为F=100N的水平向右恒力,可使物体从斜面底端由静止开始向上滑行,求(已知sin37°=0.6,cos37°=0.8,g=10m/s2) 如图所示,半径均为R,质量均为M,内表面光滑的两个完全相同的$\frac{1}{4}$圆槽A、B并排放在光滑的水平面上,图中a、c分别为A、B槽的最高点,b、b′分别为A、B槽的最低点,A槽的左端紧靠着墙壁,一个质量为m的小球C从圆槽的顶端的a点无初速度释放,求:
如图所示,半径均为R,质量均为M,内表面光滑的两个完全相同的$\frac{1}{4}$圆槽A、B并排放在光滑的水平面上,图中a、c分别为A、B槽的最高点,b、b′分别为A、B槽的最低点,A槽的左端紧靠着墙壁,一个质量为m的小球C从圆槽的顶端的a点无初速度释放,求: 如图,在水平桌面上用硬纸板做成一个斜面,使一个钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动,用一把刻度尺可以测量出钢球在水平桌面上运动的速度.具体做法是:
如图,在水平桌面上用硬纸板做成一个斜面,使一个钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动,用一把刻度尺可以测量出钢球在水平桌面上运动的速度.具体做法是: 如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )
如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.EK代表动能,E代表机械能,EP代表势能,a代表加速度,x代表路程,t代表时间,下图中能正确反映物理量之间关系的图象是( )