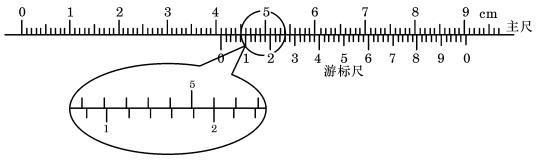
题目内容
某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50Hz的交流电源上,实验时得到一条纸带,他在纸带上便于测量的地方选取第一个计时点,在这个点下标明A,第六个点下标明B,第十一个点下标明C,第十六个点下标明D,第二十一个点下标明E.测量时发现B点已模糊不清,于是他测得AC长为14.46cm,CD长为11.15cm,DE长为13.73cm,则打C点时小车的瞬时速度大小为______m/s,小车运动的加速度大小为______m/s2.(保留三位有效数字)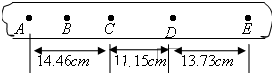

在这个点下标明A,第六个点下标明B,第十一个点下标明C,第十六个点下标明D,第二十一个点下标明E;可以看出相邻的计数点间的时间间隔为T=0.1s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小,
vC=
=0.0984m/s
设A到B之间的距离为x1,设B到C之间的距离为x2,设C到D之间的距离为x3,设D到E之间的距离为x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=
(a1+a2)
即小车运动的加速度计算表达式为:a=
a=
m/s2=2.59m/s2
故答案为:0.0984,2.59
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小,
vC=
| xAE |
| 4T |
设A到B之间的距离为x1,设B到C之间的距离为x2,设C到D之间的距离为x3,设D到E之间的距离为x4,
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=
| 1 |
| 2 |
即小车运动的加速度计算表达式为:a=
| (x4+x3-x2-x1) |
| 4T2 |
a=
| xCE-xAC |
| 4T2 |
故答案为:0.0984,2.59

练习册系列答案
相关题目



 郝双制作
郝双制作