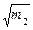题目内容
（14分）如图10所示，半径为R的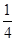
光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m2的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m1的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点。求：
（1）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少？
（2）要使小球A与小球B能发生二次碰撞，m1与m2应满足什么关系？
光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m2的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m1的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点。求：（1）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少？
（2）要使小球A与小球B能发生二次碰撞，m1与m2应满足什么关系？
（1）
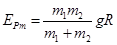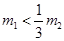
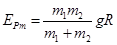（2）
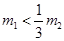
（2）（1）设A球到达圆弧底端时的速度为v0，根据机械能守恒定律有：
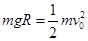……① （1分）
当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v
根据动量守恒定律有：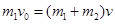
……② （2分）
根据机械能守恒定律有：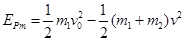
……③ （2分）
联立①②③解得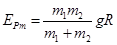： ……④ （1分）
（2）设A、B碰撞后的速度分别为v1和v2
根据动量守恒定律有：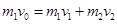
……⑤ （1分）
根据机械能守恒定律有：
……⑥ （1分）
联立⑤⑥解得：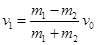
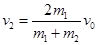（2分）
要使A、B两球能发生二次碰撞，必须满足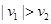
……⑨
则有：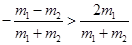
……⑩ （2分）
解得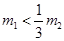： ……12 （2分）
或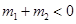
（不符合事实，舍去）
本题考查动量守恒定律和功能关系，小球由最高点到最低点，由动能定律求得最低点速度，当弹簧弹性势能最大时，两球速度相同，在与弹簧作用过程中系统机械能守恒，两小球动能的减小量转化为弹簧的弹性势能。列式求解
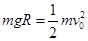……① （1分）当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v
根据动量守恒定律有：
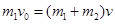……② （2分）根据机械能守恒定律有：
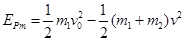……③ （2分）联立①②③解得：
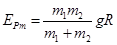……④ （1分）（2）设A、B碰撞后的速度分别为v1和v2
根据动量守恒定律有：
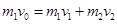……⑤ （1分）根据机械能守恒定律有：
……⑥ （1分）联立⑤⑥解得：
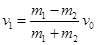
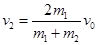（2分）要使A、B两球能发生二次碰撞，必须满足
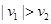……⑨则有：
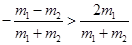……⑩ （2分）解得：
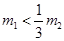……12 （2分）或
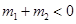（不符合事实，舍去）本题考查动量守恒定律和功能关系，小球由最高点到最低点，由动能定律求得最低点速度，当弹簧弹性势能最大时，两球速度相同，在与弹簧作用过程中系统机械能守恒，两小球动能的减小量转化为弹簧的弹性势能。列式求解
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
="1." 0×103kg/m3．若用水枪喷出的水从车后沿水平方向冲击小车的前壁，且冲击到小车前壁的水全部沿前壁流进小车中．当有质量为m="5" kg的水进入小车时，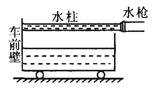
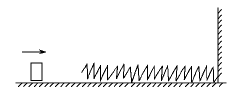
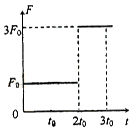
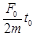
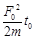
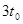时刻拉力的瞬时功率为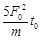
：
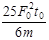
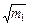