题目内容
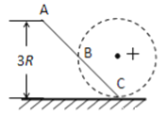
【题目】如图所示，在竖直平面内，光滑绝缘直杆AC与半径为R的圆周交于B、C两点，在圆心处有一固定的正点电荷，B点为AC的中点，C点位于圆周最低点。现有一质量为m、电荷量为q套在杆上的带负电小球（可视为质点）从A点由静止开始沿杆下滑。已知重力加速度为g，A点距过C点的水平面的竖直高度为3R，小球滑到B点时的速度大小为
。求：
（1）A、B两点间的电势差
；
（2）小球滑至C点时的速度的大小；
（3）若以C点做为零电势点，试确定A点的电势。
【答案】(1) A、B两点间的电势差
(2) 
(3) 
【解析】
考查带电粒子在复合场中运动中速度、能量问题，根据动能定理计算可得。
由动能定理有：
代入数值可解得：
B两点间的电势差
小球从B到C电场力做的总功为零，由几何关系可得BC的竖直高度为：
，根据动能定理有：
解得：
小球从A到C，重力和电场力均做正功，所以由动能定理有
，
得：
，
电场力做正功，电势能减小．又因为C点为零电势点，所以电荷-q在A点有电势能
，
有：
练习册系列答案
相关题目
