题目内容
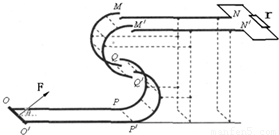
如图15所示,固定在上、下两层水平面上的平行金属导轨MN、M'N'和OP、O'P'间距都是l,二者之间固定有两组竖直半圆形轨道PQM和P'Q'M',两轨道间距也均为l,且PQM和P'Q'M'的竖直高度均为4R,两组半圆形轨道的半径均为R.轨道的QQ'端、MM'端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定.将一质量为m的金属杆沿垂直导轨方向放在下层导轨的最左端OO'位置,金属杆在与水平成θ角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好.当金属杆通过4R的距离运动到导轨末端PP'位置时其速度大小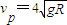 .金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计.
.金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计.(1)已知金属杆与下层导轨间的动摩擦因数为μ,求金属杆所受恒力F的大小;
(2)金属杆运动到PP'位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道PQ和P'Q',又在对接狭缝Q和Q'处无碰撞地水平进入第二组半圆形轨道QM和Q'M'的内侧,求金属杆运动到半圆轨道的最高位置MM'时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为r,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中.金属杆由第二组半圆轨道的最高位置MM'处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行.求金属杆在上层导轨上滑行的最大距离.
【答案】分析:(1)直线加速过程,受到拉力、重力、支持力和滑动摩擦力,对直线加速过程运用动能定理列式求解;
(2)导体棒沿着圆弧型光滑轨道上滑过程,只有重力做功,机械能守恒,根据守恒定律列式求解出最高点速度,然后根据向心力公式和牛顿第二定律列式求解出导体棒所受压力,最后根据牛顿第三定律求解棒对轨道的压力;
(3)对减速过程运用法拉第电磁感应定律、闭合电路欧姆定律、动量定理列式后联立求解.
解答:解:(1)导体棒加速过程中,重力和支持力不做功,只有拉力和摩擦力做功,拉力做功为W1=F?4R?cosθ,摩擦力为Ff=μFN=μ(mg-Fsinθ),
故摩擦力做功为W2=-μ(mg-Fsinθ)?4R;
根据动能定理W=△Ek,有
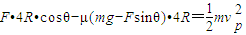
解得
F=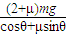
故金属杆所受恒力F的大小为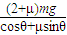 .
.
(2)设金属杆从PP′位置运动到轨道最高点位置MM′时的速度为v1,此过程根据机械能守恒定律有
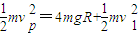
解得
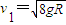
设金属杆MM′位置所受轨道压力为FM,根据牛顿第二定律,有
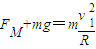
解得
FM=7mg
由牛顿第三定律可知,金属杆对轨道压力的大小F′M=7mg
故金属杆运动到半圆轨道的最高位置MM'时,它对轨道作用力的大小为7mg.
(3)金属杆在上层导轨上滑行时由于安培力作用而最终静止.设运动时间为△t,根据动量定理
BIL?△t=mv1
即
Blq=mv1
则
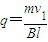
根据闭合电路欧姆定律,有
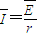
根据法拉第电磁感应定律,有
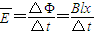
而
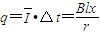
由此可得
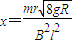
故金属杆在上层导轨上滑行的最大距离为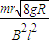 .
.
点评:本题关键是明确导体棒运动过程中的能量变化情况,然后多次运用动能定理、机械能守恒定律、动量定理列式求解.
(2)导体棒沿着圆弧型光滑轨道上滑过程,只有重力做功,机械能守恒,根据守恒定律列式求解出最高点速度,然后根据向心力公式和牛顿第二定律列式求解出导体棒所受压力,最后根据牛顿第三定律求解棒对轨道的压力;
(3)对减速过程运用法拉第电磁感应定律、闭合电路欧姆定律、动量定理列式后联立求解.
解答:解:(1)导体棒加速过程中,重力和支持力不做功,只有拉力和摩擦力做功,拉力做功为W1=F?4R?cosθ,摩擦力为Ff=μFN=μ(mg-Fsinθ),
故摩擦力做功为W2=-μ(mg-Fsinθ)?4R;
根据动能定理W=△Ek,有
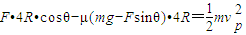
解得
F=
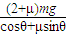
故金属杆所受恒力F的大小为
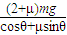 .
.(2)设金属杆从PP′位置运动到轨道最高点位置MM′时的速度为v1,此过程根据机械能守恒定律有
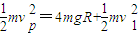
解得
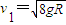
设金属杆MM′位置所受轨道压力为FM,根据牛顿第二定律,有
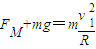
解得
FM=7mg
由牛顿第三定律可知,金属杆对轨道压力的大小F′M=7mg
故金属杆运动到半圆轨道的最高位置MM'时,它对轨道作用力的大小为7mg.
(3)金属杆在上层导轨上滑行时由于安培力作用而最终静止.设运动时间为△t,根据动量定理
BIL?△t=mv1
即
Blq=mv1
则
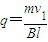
根据闭合电路欧姆定律,有
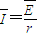
根据法拉第电磁感应定律,有
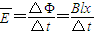
而
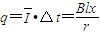
由此可得
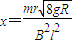
故金属杆在上层导轨上滑行的最大距离为
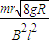 .
.点评:本题关键是明确导体棒运动过程中的能量变化情况,然后多次运用动能定理、机械能守恒定律、动量定理列式求解.

练习册系列答案
相关题目



 、
、 和
和 、
、 间距都是
间距都是 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道 和
和 ,两轨道间距也均为
,两轨道间距也均为 端、
端、 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端 位置,金属杆在与水平成
位置,金属杆在与水平成 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端 位置时其速度大小
位置时其速度大小 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小; 和
和 ,又在对接狭缝
,又在对接狭缝 和
和 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道 和
和 的内侧,求金属杆运动到半圆轨道的最高位置
的内侧,求金属杆运动到半圆轨道的最高位置 ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置