题目内容
 有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为M的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg.
有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为M的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg.(1)在求小球在A点的速度v0时,甲同学的解法是:由于小球恰好到达B点,故在B点小球的速度为零,
| 1 |
| 2 |
| v | 2 0 |
| gR |
(2)在求小球由BFA回到A点的速度时,乙同学的解法是:由于回到A点时对轨道的压力为4mg,故4mg=
m
| ||
| R |
| gR |
(3)根据题中所描绘的物理过程,求小球由B经F回到A的过程中克服摩擦力所做的功.
分析:(1)甲同学的解法是错误的,小球在最高点的临界速度不是零,靠重力提供向心力,求出临界速度,再根据动能定理求出小球在A点的初速度.
(2)乙同学的解法是错误的,在A点是竖直方向上的合力提供向心力,不是支持力提供向心力.根据牛顿第二定律求出回到A点的速度.
(3)对小球由B经F回到A的过程中运用动能定理求出小球由B经F回到A的过程中克服摩擦力所做的功.
(2)乙同学的解法是错误的,在A点是竖直方向上的合力提供向心力,不是支持力提供向心力.根据牛顿第二定律求出回到A点的速度.
(3)对小球由B经F回到A的过程中运用动能定理求出小球由B经F回到A的过程中克服摩擦力所做的功.
解答:解:不同意,两位同学的解法都错误,甲同学认为最高点的临界速度为零,实际上在最高点的临界情况是弹力为零,靠重力提供向心力,有最小速度.乙同学认为在最低点是支持力提供向心力,实际上时竖直方向上的合力提供向心力.
(1)小球恰好到达B点,在B点小球的速度不为零.
小球由AEB到B点的速度时mg=m
,vB=
由动能定理
mvB2-
mv02=-mg?2R,得v0=
.
(2)由于回到A点时对轨道压力为4mg,小球受到的合力并不是4mg.
根据牛顿定律:4mg-mg=m
,vA=
.
(3)小球由B经F回到A的过程中,
由2mgR-Wf=
mvA2-
mgR和vA=
得Wf=mgR.
答:(1)小球在A点的速度为
.
(2)回到A点的速度为
.
(3)小球由B经F回到A的过程中克服摩擦力所做的功为mgR.
(1)小球恰好到达B点,在B点小球的速度不为零.
小球由AEB到B点的速度时mg=m
| vB2 |
| R |
| gR |
由动能定理
| 1 |
| 2 |
| 1 |
| 2 |
| 5gR |
(2)由于回到A点时对轨道压力为4mg,小球受到的合力并不是4mg.
根据牛顿定律:4mg-mg=m
| vA2 |
| R |
| 3gR |
(3)小球由B经F回到A的过程中,
由2mgR-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| 3gR |
得Wf=mgR.
答:(1)小球在A点的速度为
| 5gR |
(2)回到A点的速度为
| 3gR |
(3)小球由B经F回到A的过程中克服摩擦力所做的功为mgR.
点评:解决本题的关键掌握小球在内轨道运动最高点的临界情况,以及知道做圆周运动径向的合力提供向心力.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
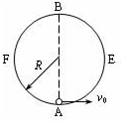 有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为m的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg.求
有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为m的小球一个水平向右的初速度,使小球沿轨道恰好运动到最高点B,小球在B点又能沿BFA回到A点,到达A点时对轨道的压力为4mg.求 有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为m的小球一个水平向右的初速度v0,使小球沿轨道恰好能过最高点B,且又能沿BFA回到A点,回到A点时对轨道的压力为4mg.不计空气阻力,重力加速度为g.求:
有一个固定竖直放置的圆形轨道,半径为R,由左右两部分组成.如图所示,右半部分AEB是光滑的,左半部分BFA是粗糙的.现在最低点A给一质量为m的小球一个水平向右的初速度v0,使小球沿轨道恰好能过最高点B,且又能沿BFA回到A点,回到A点时对轨道的压力为4mg.不计空气阻力,重力加速度为g.求:
