题目内容
 如图,弹簧的一端固定在水平面上,另一端与质量为1Kg的小球相连,小球原来处于静止状态.现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s 弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g 取10m/S2.则( )
如图,弹簧的一端固定在水平面上,另一端与质量为1Kg的小球相连,小球原来处于静止状态.现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s 弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g 取10m/S2.则( )分析:先根据运动学公式求解出位移和加速度,然后根据胡克定律确定劲度系数;
解答:解:A、小球从静止开始向上做匀加速直线运动,经0.2s 弹簧刚好恢复到原长,此时小球的速度为1m/s;
根据平均速度公式,位移:x=
t=
t=
×0.2m=0.1m;
加速度:a=
=
m/s2=5m/s2;
刚开始弹簧静止,故mg=kx,解得:k=
=
N/m=100N/m,故A正确;
B、对小球受力分析,受重力、拉力和弹力,根据牛顿第二定律,有:F-mg+k(x-
at2)=ma;
解得:F=5+250t2 (t≤0.2s)
拉力F的功率:P=Fv=Fat=(5+250t2)×5t,当t=0.2s时,拉力功率达到最大,为Pm=15W,故B正确;
C、在0~0.2s 内拉力F=5+250t2 (t≤0.2s),逐渐增加,最大为15N,位移为0.1m,故拉力功小于15N×0.1m,即小于1.5J,故C错误;
D、在0~0.2s 内拉力做正功,故小球和弹簧组成的系统机械能增加,故D错误;
故选AB.
根据平均速度公式,位移:x=
. |
| v |
| v |
| 2 |
| 1 |
| 2 |
加速度:a=
| △v |
| △t |
| 1-0 |
| 0.2 |
刚开始弹簧静止,故mg=kx,解得:k=
| mg |
| x |
| 1×10 |
| 0.1 |
B、对小球受力分析,受重力、拉力和弹力,根据牛顿第二定律,有:F-mg+k(x-
| 1 |
| 2 |
解得:F=5+250t2 (t≤0.2s)
拉力F的功率:P=Fv=Fat=(5+250t2)×5t,当t=0.2s时,拉力功率达到最大,为Pm=15W,故B正确;
C、在0~0.2s 内拉力F=5+250t2 (t≤0.2s),逐渐增加,最大为15N,位移为0.1m,故拉力功小于15N×0.1m,即小于1.5J,故C错误;
D、在0~0.2s 内拉力做正功,故小球和弹簧组成的系统机械能增加,故D错误;
故选AB.
点评:本题关键是明确小球的运动规律,然后根据运动学公式求解出小球的位移和加速度,最后对小球受力分析求解出拉力、拉力功率的表达式分析,较难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,弹簧的一端固定在水平面上,另一端与质量为1Kg的小球相连,小球原来处于静止状态.现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s 弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g 取10m/s2.则( )
如图,弹簧的一端固定在水平面上,另一端与质量为1Kg的小球相连,小球原来处于静止状态.现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s 弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g 取10m/s2.则( )| A、弹簧的劲度系数为l00N/m | B、在0~0.2s 内拉力的最大功率为15W | C、在0~0.2s 内拉力对小球做的功小于小球机械能增量 | D、在0~0.2s 内小球和弹簧组成的系统机械能守恒 |
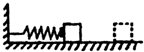 为了只用一根弹簧和一把刻度尺测定某滑块与水平桌面间的动摩擦因数μ(设μ为定值),某同学经查阅资料知:一劲度系数为k的轻弹簧由压缩量为x至恢复到原长的过程中,弹力所做的功为
为了只用一根弹簧和一把刻度尺测定某滑块与水平桌面间的动摩擦因数μ(设μ为定值),某同学经查阅资料知:一劲度系数为k的轻弹簧由压缩量为x至恢复到原长的过程中,弹力所做的功为
 .于是他设计了下列实验:
.于是他设计了下列实验: