题目内容
14.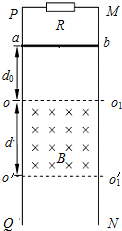 如图,竖直放置的光滑平行金属导轨MN、PQ相距L=1m,在M点和P点间接一个阻值为R=8欧姆的电阻,在两导轨间 OO1O1′O′矩形区域内有垂直导轨平面向里、宽为d=8m的匀强磁场,磁感应强度为B=1T.一质量为m=0.1kg,电阻为r=2欧姆的导体棒ab垂直搁在导轨上,与磁场上边边界相距d0=2m.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的电接触且下落过程中始终保持水平,导轨电阻不计).求:
如图,竖直放置的光滑平行金属导轨MN、PQ相距L=1m,在M点和P点间接一个阻值为R=8欧姆的电阻,在两导轨间 OO1O1′O′矩形区域内有垂直导轨平面向里、宽为d=8m的匀强磁场,磁感应强度为B=1T.一质量为m=0.1kg,电阻为r=2欧姆的导体棒ab垂直搁在导轨上,与磁场上边边界相距d0=2m.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的电接触且下落过程中始终保持水平,导轨电阻不计).求:(1)棒ab在离开磁场下边界时的速度;
(2)棒ab在通过磁场区的过程中产生的焦耳热;
(3)若改变d0,棒ab在离开磁场前仍然做匀速直线运动,试分析讨论ab棒在磁场中可能出现的运动情况.
分析 (1)导体棒做匀速直线运动,处于平衡状态,由安培力公式及平衡条件可以求出棒离开下边界时的速度.
(2)由能量守恒定律可以求出金属棒产生的焦耳热.
(3)根据棒进入磁场时的速度大小,讨论棒在磁场中的运动情况.
解答 解:(1)棒匀速时 mg=BIL
解得 $I=\frac{{BL{v_0}}}{{R+{r_{\;}}}}$
所以 $v=\frac{{mg({R+{r_{\;}}})}}{{{B^2}{L^2}}}$=10m/s
(2)根据动能定理可得 $mg((d+d_0)-W_{\;}=\frac{1}{2}mv^2$
由于 Q=W
所以 ${Q_r}={\frac{r}{R+r}}_{\;}Q$=1J
(3)刚好匀速时由 v2=2gd0d0=5m
当d0>5m,棒ab刚进入磁场时受到的安培力F安>mg 做先减速后匀速运动
当d0=5m,棒ab刚进入磁场时受到的安培力F安=mg 一直匀速运动
当d0<5m,棒ab刚进入磁场时受到的安培力F安<mg 做先加速后匀速运动
答:(1)棒ab离开磁场的下边界时的速度为10m/s.
(2)棒ab在通过磁场区的过程中产生的焦耳热为1J.
(3)当d0>5m,棒ab刚进入磁场时受到的安培力F安>mg 做先减速后匀速运动
当d0=5m,棒ab刚进入磁场时受到的安培力F安=mg 一直匀速运动
当d0<5m,棒ab刚进入磁场时受到的安培力F安<mg 做先加速后匀速运动
点评 本题最后一问是本题的难点,根据棒进入磁场时的速度进行分析讨论是正确解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.关于超重和失重,下列说法正确的是( )
| A. | 超重就是物体受到的重力增大了 | |
| B. | 失重就是物体受到的重力减小了 | |
| C. | 完全失重就是物体受到的重力为零 | |
| D. | 无论超重、失重,物体受到的重力都不变 |
5.人类一直不断地对宇宙追求探索着,关于宇宙天体学说正确的是( )
| A. | 日心说代表人物是托勒密 | |
| B. | 地心说是正确的,日心说是错误的 | |
| C. | 日心说被人们所接受的原因是以太阳为中心,许多问题都可以解决,行星运动也变得简单了 | |
| D. | 太阳从东边升起,从西边落下,所以太阳绕地球运动 |
9.发电的基本原理是电磁感应.发现电磁感应现象的科学家是( )
| A. | 安培 | B. | 奥斯特 | C. | 麦克斯韦 | D. | 法拉第 |
19.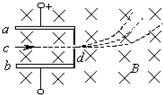 如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
 如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )
如图所示,a、b是一对平行的金属板,分别接到直流电源的两极上,右边有一档板,正中间开有一小孔d.在较大的空间范围内存在着匀强磁场,磁感应强度大小为B,方向垂直纸面向里,而在a、b两板间还存在着匀强电场.从两板左侧正中的中点c处射入一束正离子,这些正离子都沿直线运动到右侧,从d孔射出后分成3束.则这些正离子的 (重力忽略)( )| A. | 速度一定都相同 | B. | 质量一定有3种不同的数值 | ||
| C. | 电量一定有3种不同的数值 | D. | 比荷($\frac{q}{m}$)一定相同数值 |
6.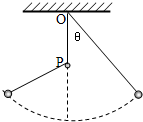 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
 如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳一端系一小球,另一端固定于O点,在O点正下方的P点钉一颗钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )| A. | 小球的瞬时速度突然变大 | B. | 小球的加速度突然变大 | ||
| C. | 球的所受的向心力突然变小 | D. | 悬线所受的拉力突然变大 |
3.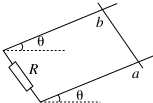 处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
 处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )
处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.对导轨光滑和粗糙两种情况进行比较,当两次下滑的位移相同时,则有( )| A. | 重力势能的减小量相同 | B. | 机械能的变化量相同 | ||
| C. | 磁通量的变化量相同 | D. | 安培力做功相同 |
4.物体在万有引力场中具有的势能叫做引力势能,取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距质量为M0的引力源中心为r0时,其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为引力常数).一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行,已知地球的质量为M,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从r1逐渐减小到r2,若在这个过程中空气阻力做功为Wt,则在下面给出的Wt的四个表达式中正确的是( )
| A. | Wt=-$\frac{GMm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) | B. | Wt=-GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | C. | Wt=-$\frac{GMm}{2}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) | D. | Wt=-$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) |