题目内容
如图所示，一个圆环以竖直方向直径AB为轴匀速转动，环上的P、Q两点和环心的连线与竖直方向所成的角分别为600和300，则P、Q两点转动的角速度之比为____________，P、Q两点的线速度大小之比为____________。
1：1；
P、Q两点以它的直径AB为轴做匀速转动，它们的角速度相同都为ω，即角速度之比为1:1
所以P点转动的半径r1=Rsin60°=
R，Q点转动的半径r2=Rsin30°=
R，
根据v=ωr得：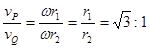
，即圆环上P、Q两点的线速度大小之比是
故答案为：1：1；
所以P点转动的半径r1=Rsin60°=
R，Q点转动的半径r2=Rsin30°=R，根据v=ωr得：
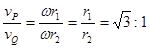，即圆环上P、Q两点的线速度大小之比是故答案为：1：1；
练习册系列答案
阅读快车系列答案
相关题目
1，木板与地面间的动摩擦因数
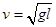向右运动，在A处环被挡住而停下的瞬间，绳子所受拉力为多少？在以后的运动过程中，球是先碰墙还是先碰地？第一次的碰撞点离B点的距离是多少？（已知A处离墙的水平距离为l，球离地的高度h=2l）
外运动?