题目内容
【题目】如图所示,两平行金属板A、B长8cm,两极板间距离d=8cm,A极板比B极板电势高300V,一电荷量q=![]() ,质量m=
,质量m=![]() 的带电正粒子,沿电场中心线RO垂直电场线飞入电场,初速度
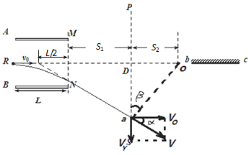
的带电正粒子,沿电场中心线RO垂直电场线飞入电场,初速度![]() ,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上,不计粒子重力(静电力常量
,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上,不计粒子重力(静电力常量![]() )
)
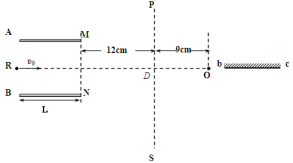
(1)求粒子穿过界面MN时偏离中心线RO的距离多远?到达PS界面时离D点多远?
(2)确定点电荷Q的电性并求其电荷量的大小
【答案】(1)0.03,0.12m(2)Q=1.04×10-8C,且Q带负
【解析】
试题分析:(1)粒子穿过界面MN时偏离中心线RO的距离(侧向位移)![]() ,
,![]() ①
①![]() ②,
②,![]() ③,联立①②③解得
③,联立①②③解得![]()
带电粒子在离开电场后将做匀速直线运动,其运动轨迹与PS线交于a点,设a到中心线的距离为Y,
则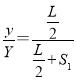
解得:![]() ;
;
(2)带电粒子到达a处时,沿v0方向的速度大小为![]()
垂直v0方向的速度大小为![]()
如图,![]() ,可知速度v方向垂直于Oa
,可知速度v方向垂直于Oa
根据题意可知,该带电粒子在穿过界面PS后将绕点电荷Q做匀速圆周运动,且半径等于Oa的长度,即
![]() ,代入数据解得:
,代入数据解得:![]() ,
,
粒子到达a点时的速度大小为![]() ;
;
由库仑定律和牛顿第二定律得![]() ;代入数值解:Q=1.04×10-8C,且Q带负
;代入数值解:Q=1.04×10-8C,且Q带负

练习册系列答案
相关题目