题目内容
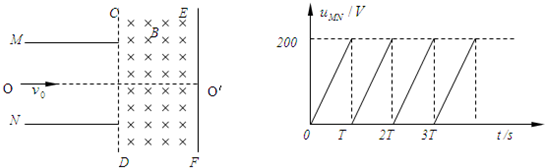
 如图所示,带正电的小物块静止在粗糙绝缘的水平面上,小物块的比荷为k=1,与水平面间的动摩擦因数为μ=0.15.在物块右侧距物块L=1m处有一范围足够大的匀强场区,场区内存在相互垂直的匀强电场和匀强磁场,已知匀强电场的方向竖直向上,场强大小恰好等于当地重力加速度的大小,匀强磁场垂直纸面向里,磁感应强度为B=0.4T.现给物块一水平向右的初速度,使其沿水平面运动并进入右侧场区,当物块从场区飞出后恰好能落到出发点.设运动过程中物块带电量保持不变,重力加速度为g=10m/s2.求:
如图所示,带正电的小物块静止在粗糙绝缘的水平面上,小物块的比荷为k=1,与水平面间的动摩擦因数为μ=0.15.在物块右侧距物块L=1m处有一范围足够大的匀强场区,场区内存在相互垂直的匀强电场和匀强磁场,已知匀强电场的方向竖直向上,场强大小恰好等于当地重力加速度的大小,匀强磁场垂直纸面向里,磁感应强度为B=0.4T.现给物块一水平向右的初速度,使其沿水平面运动并进入右侧场区,当物块从场区飞出后恰好能落到出发点.设运动过程中物块带电量保持不变,重力加速度为g=10m/s2.求:(1)物块刚进入场区时的速度;
(2)物块从开始运动到刚好进入场区所用的时间.
分析:根据题目提供的条件,物体在复合场中运动时,重力大小等于电场力,物体在洛伦兹力的做下做圆周运动,写出其运动学的方程;物体离开场区后做平抛运动,经过时间t落地,按照水平方向和竖直方向分解运动即可求得物体的初速度;
物体开始运动的一段时间内做匀加速运动,使用牛顿第二定律和运动学的公式即可.
物体开始运动的一段时间内做匀加速运动,使用牛顿第二定律和运动学的公式即可.
解答:解:设物体的质量为m,带电量为q,根据题中的条件可得:
Eq=mg ①
即带电物体进入场区后恰好在竖直平面内做匀速圆周运动,离开场区后做平抛运动.
设物体进入场区时的速度为v1,做圆周运动的半径为R,则:
Bqv1=m
②
物体离开场区后做平抛运动,经过时间t落地,依题意应满足:
2R=
gt2 ③
L=v1t ④
解②③④可得:v1=
(2)设物体开始运动时的速度为v0,加速度为a,进入场区前使用的时间为t0,则:
-μmg=ma ⑤
-
=2aL ⑥
L=
?t0 ⑦
解⑤⑥⑦可得:t0=
答:(1)物块刚进入场区时的速度v1=
;
(2)物块从开始运动到刚好进入场区所用的时间t0=
.
Eq=mg ①
即带电物体进入场区后恰好在竖直平面内做匀速圆周运动,离开场区后做平抛运动.
设物体进入场区时的速度为v1,做圆周运动的半径为R,则:
Bqv1=m
| ||
| R |
物体离开场区后做平抛运动,经过时间t落地,依题意应满足:
2R=
| 1 |
| 2 |
L=v1t ④
解②③④可得:v1=
| 3 |
| ||
(2)设物体开始运动时的速度为v0,加速度为a,进入场区前使用的时间为t0,则:
-μmg=ma ⑤
| v | 2 1 |
| v | 2 0 |
L=
| v0+v1 |
| 2 |
解⑤⑥⑦可得:t0=
[(
| ||||||||||
| μg |
答:(1)物块刚进入场区时的速度v1=
| 3 |
| ||
(2)物块从开始运动到刚好进入场区所用的时间t0=
[(
| ||||||||||
| μg |
点评:本题考查带电粒子在电场与磁场的综合应用.突出带电粒子在磁场中始终不做功.判断出物体在复合场中运动时,重力大小等于电场力,物体在洛伦兹力的做下做圆周运动是解题的关键,难度适中.

练习册系列答案
相关题目
 如图所示,带正电的电荷固定于Q点,电子在静电力作用下沿顺时针方向做以Q点为焦点的椭圆运动,O为椭圆的中心,M、P、N为椭圆上的三点,M和N分别是轨道上离Q点最近和最远的点,则电子在运动的过程中( )
如图所示,带正电的电荷固定于Q点,电子在静电力作用下沿顺时针方向做以Q点为焦点的椭圆运动,O为椭圆的中心,M、P、N为椭圆上的三点,M和N分别是轨道上离Q点最近和最远的点,则电子在运动的过程中( ) 如图所示,带正电的点电荷固定于Q点,电子在库仑力的作用下沿顺时针方向做以Q点为焦点的椭圆运动,O为椭圆的中心,M、P、N为椭圆上的三点,M和N分别是轨道上离Q点最近和最远的点,则电子在运动的过程中( )
如图所示,带正电的点电荷固定于Q点,电子在库仑力的作用下沿顺时针方向做以Q点为焦点的椭圆运动,O为椭圆的中心,M、P、N为椭圆上的三点,M和N分别是轨道上离Q点最近和最远的点,则电子在运动的过程中( ) (2009?徐汇区二模)如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下,沿顺时针方向做以Q为一焦点的椭圆运动.O为椭圆的中心,M、P、N为椭圆上的三个点,M和N分别是椭圆上离Q最近和最远的点.则以下说法中正确的是( )
(2009?徐汇区二模)如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下,沿顺时针方向做以Q为一焦点的椭圆运动.O为椭圆的中心,M、P、N为椭圆上的三个点,M和N分别是椭圆上离Q最近和最远的点.则以下说法中正确的是( )