题目内容
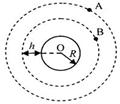
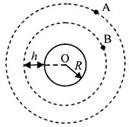
 如图所示,A表示地球,它的半径为R,自转角速度为ω1,表面重力加速度为g,一人造卫星B在赤道平面内绕圆轨道运行,离地面的离度为H,求:
如图所示,A表示地球,它的半径为R,自转角速度为ω1,表面重力加速度为g,一人造卫星B在赤道平面内绕圆轨道运行,离地面的离度为H,求:①卫星B的运动角速度ω2.
②假设卫星B绕行方向与地球的自转方向相同,某时刻地球的同步卫星正好在B的正上方离B最近,那么从这一时刻起,还要最少经过多长时间,B能运动到同步卫星的正下方和同步卫星最近?
分析:(1)卫星B做圆周运动的向心力由A对它的万有引力提供,由万有引力公式及向心力公式列方程即可求出卫星的角速度.
(2)卫星B与同步卫星转过的圆心角之差等于2π弧度时,B能再次运动到同步卫星的正下方和同步卫星最近.
(2)卫星B与同步卫星转过的圆心角之差等于2π弧度时,B能再次运动到同步卫星的正下方和同步卫星最近.
解答:解:(1)设地球A的质量是M,卫星B的质量为m,
卫星B绕地球做圆周运动的半径r=R+H,
卫星B做圆周运动的向心力由A对它的万有引力提供,
由牛顿第二定律可得:G
=mω22(R+H)①,
地球表面的物体m′受到的重力等于地球对它的万有引力,
即:m′g=G
②,
由①②解得:ω2=R
③;
(2)设经过时间t,B能再次运动到同步卫星的正下方和同步卫星最近,
此时卫星B与同步卫星转过的圆心角之差等于2π弧度,
即:ω2t-ω1t=2π ④,
由③④解得:t=
;
答:(1)卫星B的运动角速度ω2=R
.
(2)经过时间
B能运动到同步卫星的正下方和同步卫星最近.
卫星B绕地球做圆周运动的半径r=R+H,
卫星B做圆周运动的向心力由A对它的万有引力提供,
由牛顿第二定律可得:G
| Mm |
| (R+H)2 |
地球表面的物体m′受到的重力等于地球对它的万有引力,
即:m′g=G
| Mm′ |
| R2 |
由①②解得:ω2=R
|
(2)设经过时间t,B能再次运动到同步卫星的正下方和同步卫星最近,
此时卫星B与同步卫星转过的圆心角之差等于2π弧度,
即:ω2t-ω1t=2π ④,
由③④解得:t=
| 2π | ||||
R
|
答:(1)卫星B的运动角速度ω2=R
|
(2)经过时间
| 2π | ||||
R
|
点评:知道万有引力提供向心力,熟练应用万有引力公式与向心力公式列方程即可求出卫星的角速度;知道两卫星转过的圆心角之差是2π弧度是正确解答第二问的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目