题目内容
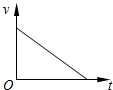
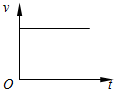
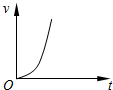
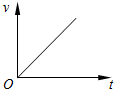
4.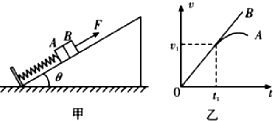 如图甲所示,平行于光滑固定斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B在斜面上紧靠着物块A但不粘连,物块A、B质量均为m.初始时两物块均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,两物块的v-t图象如图乙所示(t1时刻图线A、B相切),己知重力加速度为g,则下列说法正确的是( )
如图甲所示,平行于光滑固定斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B在斜面上紧靠着物块A但不粘连,物块A、B质量均为m.初始时两物块均静止.现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,两物块的v-t图象如图乙所示(t1时刻图线A、B相切),己知重力加速度为g,则下列说法正确的是( )| A. | A、B分离前,A、B和弹簧系统机械能增加,A和弹簧系统机械能增加 | |
| B. | 力F的最小值为m(gsinθ+a) | |
| C. | A达到最大速度时的位移为$\frac{mgsinθ}{k}$ | |
| D. | t1=$\sqrt{\frac{2(mgsinθ-ma)}{ak}}$时A、B分离 |
分析 A的速度最大时加速度为零,根据胡克定律求出A达到最大速度时的位移;根据牛顿第二定律求出拉力F的最小值.由图读出,t1时刻A、B开始分离,对A根据牛顿第二定律和运动学公式求解t1.根据功能关系分析能量如何转化.
解答 解:A、A、B分离前,F做正功,根据功能关系得知,A、B和弹簧系统机械能增加,而B对A的压力做负功,A和弹簧系统机械能减小.故A错误.
B、对AB整体,根据牛顿第二定律得:F-2mgsinθ+kx=2ma,
得:F=2mgsinθ-kx+2ma,
则知开始时F最小,此时有:2mgsinθ=kx,得F的最小值为:F=2ma,故B错误.
C、由图知,A的加速度为零,速度最大,根据牛顿第二定律和胡克定律得:mgsinθ=kx,
得:$x=\frac{mgsinθ}{k}$,故C正确.
D、由图读出,t1时刻A、B开始分离,对A根据牛顿第二定律:kx-mgsinθ=ma
开始时有:2mgsinθ=kx0,
又x0-x=$\frac{1}{2}a{t}_{1}^{2}$
联立以三式得:t1=$\sqrt{\frac{2(mgsinθ-ma)}{ak}}$.故D正确.
故选:CD
点评 从受力角度看,两物体分离的条件是两物体间的正压力为0.从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在物理学发展的过程中,许多物理学家的科学研究推动了人类文明的进程.以下几个说法中正确的是( )
| A. | 安培最早测定了元电荷 e的数值 | |
| B. | 奥斯特首先发现了电流的磁效应 | |
| C. | 富兰克林提出的分子电流假说,揭示了磁现象的电本质 | |
| D. | 法拉第在前人工作的基础上,通过实验研究确认了库仑定律 |
19.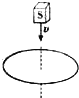 1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的离子,即“磁单极子”,1982年,美国物理学家卡布莱设计了一个寻找磁单极子的实验:他设想,如果一个只有S极的磁单极子从上向下穿过如图所示的闭合超导线圈,那么,从上向下看,这个线圈中将出现( )
1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的离子,即“磁单极子”,1982年,美国物理学家卡布莱设计了一个寻找磁单极子的实验:他设想,如果一个只有S极的磁单极子从上向下穿过如图所示的闭合超导线圈,那么,从上向下看,这个线圈中将出现( )
 1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的离子,即“磁单极子”,1982年,美国物理学家卡布莱设计了一个寻找磁单极子的实验:他设想,如果一个只有S极的磁单极子从上向下穿过如图所示的闭合超导线圈,那么,从上向下看,这个线圈中将出现( )
1931年英国物理学家狄拉克从理论上预言:存在只有一个磁极的离子,即“磁单极子”,1982年,美国物理学家卡布莱设计了一个寻找磁单极子的实验:他设想,如果一个只有S极的磁单极子从上向下穿过如图所示的闭合超导线圈,那么,从上向下看,这个线圈中将出现( )| A. | 先是逆时针方向的感应电流,然后是顺时针方向的感应电流 | |
| B. | 先是顺时针方向的感应电流,然后是逆时针方向的感应电流 | |
| C. | 顺时针方向的持续流动的感应电流 | |
| D. | 逆时针方向的持续流动的感应电流 |
9.“空间站”是科学家进行天文探测和科学试验的特殊而又重要的场所.假设某“空间站”正在地球赤道平面内的圆周轨道上运行,其离地高度为同步卫星离地高度的十分之一,且运行方向与地球自转方向一致.下列关于该“空间站”的说法正确的有( )
| A. | 运行的加速度不等于其所在高度处的重力加速度 | |
| B. | 运行的速度等于同步卫星运行速度的$\sqrt{10}$倍 | |
| C. | 站在地球赤道上的人观察到它向东运动 | |
| D. | 在“空间站”内工作的宇航员因受到平衡力而在其中悬浮或静止 |
13.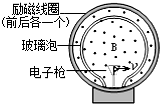 如图所示为洛伦兹力演示仪的结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直?电子速度的大小和磁场强弱可分别由通过电子枪的加速电压和励磁线圈的电流来调节.下列说法正确的是( )
如图所示为洛伦兹力演示仪的结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直?电子速度的大小和磁场强弱可分别由通过电子枪的加速电压和励磁线圈的电流来调节.下列说法正确的是( )
 如图所示为洛伦兹力演示仪的结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直?电子速度的大小和磁场强弱可分别由通过电子枪的加速电压和励磁线圈的电流来调节.下列说法正确的是( )
如图所示为洛伦兹力演示仪的结构图.若励磁线圈产生的匀强磁场方向垂直纸面向外,电子束由电子枪产生,其速度方向与磁场方向垂直?电子速度的大小和磁场强弱可分别由通过电子枪的加速电压和励磁线圈的电流来调节.下列说法正确的是( )| A. | 仅减小励磁线圈中电流,电子束径迹的半径变小 | |
| B. | 仅降低电子枪加速电压,电子束径迹的半径变小 | |
| C. | 仅减小励磁线圈中电流,电子做圆周运动的周期将变小 | |
| D. | 仅降低电子枪加速电压,电子做圆周运动的周期将变小 |
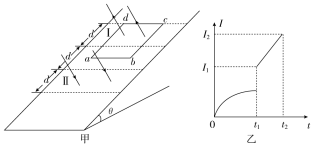
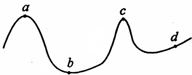 一质点以匀速率在水平面上做曲线运动,其轨迹如图所示.从图中可以看出,质点在a、b、c、d 四点处加速度最大的点是( )
一质点以匀速率在水平面上做曲线运动,其轨迹如图所示.从图中可以看出,质点在a、b、c、d 四点处加速度最大的点是( )