题目内容
长木板M带着小物块m一起以速度v沿光滑面运动,M与远处墙壁碰撞时间极短且碰后M等速率返回,m与M间的接触面间的动摩擦因数为μ,若M>m,则最后的共同速度为多少?(设M足够长)从m在M上相对滑动起到相对静止一共历时多少?
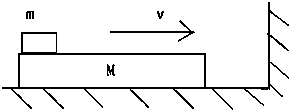

分析:长木板与墙发生碰撞后以原速率弹回,此后木板与物块所受的合外力为零,总动量守恒,根据动量守恒定律求解长木板与物块的共同速度,并确定出速度的方向.
对m或M,运用动量定理求解时间.
对m或M,运用动量定理求解时间.
解答:解:M与墙壁碰撞后,m与M组成的系统所受的合外力为零,系统的动量守恒,取向左方向为正方向,根据动量守恒定律得:
Mv-mv=(M+m)v′
则得共同速度为:v′=
v,方向水平向左;
对M,取向右方向为正方向,根据动量定理得:
-μmgt=Mv′-Mv
得:t=
=
答:最后的共同速度为
v,方向水平向左;从m在M上相对滑动起到相对静止一共历时为
.
Mv-mv=(M+m)v′
则得共同速度为:v′=
| M-m |
| M+m |
对M,取向右方向为正方向,根据动量定理得:
-μmgt=Mv′-Mv
得:t=
| M(v-v′) |
| μmg |
| 2Mv |
| μ(M+m)g |
答:最后的共同速度为
| M-m |
| M+m |
| 2Mv |
| μ(M+m)g |
点评:对于两个或两个物体相互作用的问题,首先考虑能否运用守恒定律,求时间,也可以牛顿第二定律和运动学公式结合求解.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
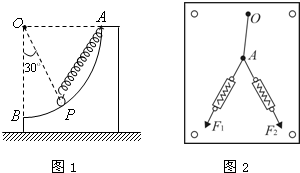 (1)一轻弹簧原长为10cm,把它上端固定,下端悬挂一重为0.5N的钩码,静止时它的长度为12cm,弹簧的劲度系数为
(1)一轻弹簧原长为10cm,把它上端固定,下端悬挂一重为0.5N的钩码,静止时它的长度为12cm,弹簧的劲度系数为