题目内容
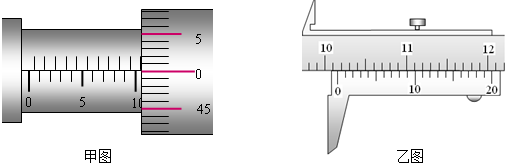
(2009?江门二模)(1)如图所示,甲图中螺旋测微器的读数为
(2)学校实验小组在“验证牛顿第二定律”的实验中,图(甲)为实验装置简图.(所用交变电流的频率为50Hz).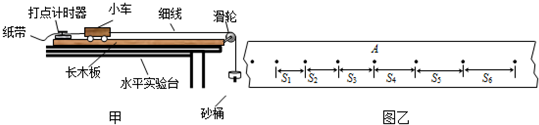
(一)同学们在进行实验时,为了减小实验时的系统误差,使分析数据时可以认为砂桶的重力等于小车所受的合外力,你认为应采取的措施有:
①
(二)如图乙所示是某小组在做实验中,由打点计时器得到的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm,则A点处瞬时速度的大小是
,加速度的大小是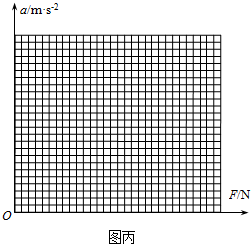
(三)另一小组在该实验中得到了如下一组实验数据:
①请在图丙所示的坐标中画出a-F的图线
②从图中可以发现实验操作中存在的问题可能是
A.实验没有平衡摩擦力
B.实验中平衡摩擦力时木板倾角过小
C.实验中平衡摩擦力时木板倾角过大
D.实验中小车质量发生变化.
10.501
10.501
mm,乙图中游标卡尺的读数为10.155
10.155
cm.
(2)学校实验小组在“验证牛顿第二定律”的实验中,图(甲)为实验装置简图.(所用交变电流的频率为50Hz).

(一)同学们在进行实验时,为了减小实验时的系统误差,使分析数据时可以认为砂桶的重力等于小车所受的合外力,你认为应采取的措施有:
①
将长木板一端垫起,让小车重力
沿斜面的分力平衡摩擦阻力
沿斜面的分力平衡摩擦阻力
将长木板一端垫起,让小车重力
沿斜面的分力平衡摩擦阻力
;②沿斜面的分力平衡摩擦阻力
小车质量远大于沙桶的总质量
小车质量远大于沙桶的总质量
.(二)如图乙所示是某小组在做实验中,由打点计时器得到的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm,则A点处瞬时速度的大小是
0.86
0.86
m/s,小车运动的加速度计算表达式为| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
0.64
0.64
m/s2(计算结果保留两位有效数字).
(三)另一小组在该实验中得到了如下一组实验数据:
| F/N | 0.196 | 0.294 | 0.392 | 0.490 | 0.588 |
| a/m?s-2 | 0.25 | 0.58 | 0.90 | 1.20 | 1.53 |
②从图中可以发现实验操作中存在的问题可能是
AB
AB
填字母序号)A.实验没有平衡摩擦力
B.实验中平衡摩擦力时木板倾角过小
C.实验中平衡摩擦力时木板倾角过大
D.实验中小车质量发生变化.
分析:(1)游标卡尺读数的方法是主尺读数加上游标读数,不需估读.螺旋测微器的读数方法是固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读.
(2)小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对钩码来说:mg-Ma=ma,即:mg=(M+m)a,如果用钩码的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量.
纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
根据所提供数据,采用描点法可正确画出图象;根据所画图象的特点,明确两坐标轴的含义,可正确解答.
(2)小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对钩码来说:mg-Ma=ma,即:mg=(M+m)a,如果用钩码的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量.
纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
根据所提供数据,采用描点法可正确画出图象;根据所画图象的特点,明确两坐标轴的含义,可正确解答.
解答:解:(1)螺旋测微器的固定刻度读数为10.5mm,可动刻度读数为0.01×0.1mm=0.001mm,所以最终读数为10.501mm.
游标卡尺的固定刻度读数为101mm,游标读数为0.05×11mm=0.55mm,所以最终读数为101.55mm=10.155cm
(2)(一)小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
其次:设小车质量M,钩码质量m,整体的加速度为a,绳上的拉力为F,则:对小车有:F=Ma;对钩码有:mg-F=ma,即:mg=(M+m)a;
如果用钩码的重力表示小车受到的合外力,则要求:Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量,这样两者才能近似相等.
(二)利用匀变速直线运动的推论得:
vA=
=0.86m/s.
由于相邻的计数点间的位移之差不等,故采用逐差法求解加速度.
小车运动的加速度计算表达式为a=
代入数据得a=0.64m/s2.
(三))①根据所提供数据,采用描点法可正确画出图象如下所示:
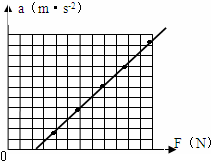
②由图象可知,当开始小车存在拉力时,加速度确为零,根据牛顿第二定律可知,此时小车应该受到摩擦力作用,因此实验中存在是问题是没有平衡摩擦力或者平衡的不够,故CD错误,AB正确.
故选AB.
故答案为:(1)10.501,10.155
(2)(一)①将长木板一端垫起,让小车重力
沿斜面的分力平衡摩擦阻力;
②小车质量远大于沙桶的总质量.
(二)0.86,
,0.64
(三)如图,AB.
游标卡尺的固定刻度读数为101mm,游标读数为0.05×11mm=0.55mm,所以最终读数为101.55mm=10.155cm
(2)(一)小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
其次:设小车质量M,钩码质量m,整体的加速度为a,绳上的拉力为F,则:对小车有:F=Ma;对钩码有:mg-F=ma,即:mg=(M+m)a;
如果用钩码的重力表示小车受到的合外力,则要求:Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量,这样两者才能近似相等.
(二)利用匀变速直线运动的推论得:
vA=
| s3+s4 |
| 2t |
由于相邻的计数点间的位移之差不等,故采用逐差法求解加速度.
小车运动的加速度计算表达式为a=
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
代入数据得a=0.64m/s2.
(三))①根据所提供数据,采用描点法可正确画出图象如下所示:
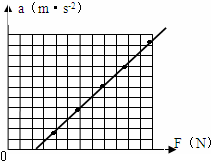
②由图象可知,当开始小车存在拉力时,加速度确为零,根据牛顿第二定律可知,此时小车应该受到摩擦力作用,因此实验中存在是问题是没有平衡摩擦力或者平衡的不够,故CD错误,AB正确.
故选AB.
故答案为:(1)10.501,10.155
(2)(一)①将长木板一端垫起,让小车重力
沿斜面的分力平衡摩擦阻力;
②小车质量远大于沙桶的总质量.
(二)0.86,
| (s4+s5+s6)-(s1+s2+s3) |
| 9T2 |
(三)如图,AB.
点评:(1)解决本题的关键掌握游标卡尺和螺旋测微器的读数方法,游标卡尺读数的方法是主尺读数加上游标读数,不需估读.螺旋测微器的读数方法是固定刻度读数加上可动刻度读数,在读可动刻度读数时需估读.
(2)要明确此题在验证合外力的功与动能变化间的关系中用到的原理,围绕原理,记忆需要测量的物理量及实验时的注意事项.要注意单位的换算和有效数字的保留.
能够运用逐差法求解加速度.
(2)要明确此题在验证合外力的功与动能变化间的关系中用到的原理,围绕原理,记忆需要测量的物理量及实验时的注意事项.要注意单位的换算和有效数字的保留.
能够运用逐差法求解加速度.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (2009?江门二模)在图中所示的电路中,当滑动变阻器的滑动触片向 b端移动时,正确的是( )
(2009?江门二模)在图中所示的电路中,当滑动变阻器的滑动触片向 b端移动时,正确的是( )