��Ŀ����
�������������������ܸ߿�ϡ���������������ã��Ƶ�����ת�Ĺ���뾶��������С���ڰ뾶�����仯�����У����ǵ��˶����ɽ��Ƶ�������Բ���˶��������ڽϴ�Ĺ���뾶r1��ʱ�������ٶ�Ϊv1������ΪT1�������ڽ�С�Ĺ���뾶r2��ʱ�������ٶ�Ϊv2������ΪT2�������ǵĹ�ϵ�ǣ�������
������������������������У������ܵ�ϡ���������������ã����˶�����뾶����С���������������ṩ�������г���ʽ���ж����ٶȡ����ڵı仯��
����⣺�������������ṩ�������г���ʽ
=
=
��ã�v=
������r1��r2������v1��v2��
T=2��
������r1��r2������T1��T2��
��ѡC��
| GMm |
| r2 |
| mv2 |
| r |
| m?4��2r |
| T2 |
��ã�v=
|
T=2��
|
��ѡC��
�������������Ĺؼ��������������ṩ������������ݸù����ж����ٶȡ����ٶȡ����ڡ����ļ��ٶ������뾶�Ĺ�ϵ��

��ϰ��ϵ�д�
�����Ŀ
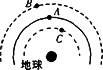
 2004��12��19�����ű�����һ����ΪKEO���������ǽ���2007�����̫�գ�����Я�������˵����Ժ���Ѫ�����е���5����ص��棬����ʱ��������21���͵�������Ϣ��������ѱ����Ϲ��̿�����֯���롰��ʮһ���ͼƻ����ġ�δ����������ɽ��Լ����ɻ�Ŀ�ꡢ��ֵ�ۡ����ʽ������ȣ�д�����Ը�5������������ڴ���������������ʱ�䳤�õ������Ժͷ��ص���ı�Ȼ�ԣ���ѧ���ڴ������ϰ�װ��������ܵ�С���������ͼ��ʾ�У�AΪ�������36000km��ͬ�������B��CΪ���������������壨̫��������ȣ�����Ӱ�������ƫ���λ�ã�Ҫʹ���ص�ͬ������ϣ�Ӧ��������
2004��12��19�����ű�����һ����ΪKEO���������ǽ���2007�����̫�գ�����Я�������˵����Ժ���Ѫ�����е���5����ص��棬����ʱ��������21���͵�������Ϣ��������ѱ����Ϲ��̿�����֯���롰��ʮһ���ͼƻ����ġ�δ����������ɽ��Լ����ɻ�Ŀ�ꡢ��ֵ�ۡ����ʽ������ȣ�д�����Ը�5������������ڴ���������������ʱ�䳤�õ������Ժͷ��ص���ı�Ȼ�ԣ���ѧ���ڴ������ϰ�װ��������ܵ�С���������ͼ��ʾ�У�AΪ�������36000km��ͬ�������B��CΪ���������������壨̫��������ȣ�����Ӱ�������ƫ���λ�ã�Ҫʹ���ص�ͬ������ϣ�Ӧ�������� ��ʱ�������ٶ�Ϊ
��ʱ�������ٶ�Ϊ ������Ϊ
������Ϊ �������ڽ�С�Ĺ���뾶
�������ڽ�С�Ĺ���뾶 ��ʱ�������ٶ�Ϊ
��ʱ�������ٶ�Ϊ ������Ϊ
������Ϊ �������ǵĹ�ϵ��
�������ǵĹ�ϵ�� ��
��
 ��
��
 ��
��