题目内容
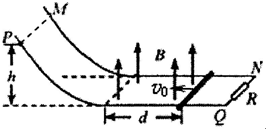 如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分和水平部分均光滑,二者平滑连接.右端接一个阻值为R的定值电阻.水平部分导轨左边区域有宽度为d的匀强磁场区域,磁场方向竖直向上,磁感应强度大小为B.质量为m、电阻也为R的金属棒从磁场区域的右边界以平行于水平导轨的初速度v0进入磁场,离开磁场后沿弯曲轨道上升h高度时速度变为零,已知金属棒与导轨间接触良好,则金属棒穿过磁场区域的过程中(重力加速度为g)( )
如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分和水平部分均光滑,二者平滑连接.右端接一个阻值为R的定值电阻.水平部分导轨左边区域有宽度为d的匀强磁场区域,磁场方向竖直向上,磁感应强度大小为B.质量为m、电阻也为R的金属棒从磁场区域的右边界以平行于水平导轨的初速度v0进入磁场,离开磁场后沿弯曲轨道上升h高度时速度变为零,已知金属棒与导轨间接触良好,则金属棒穿过磁场区域的过程中(重力加速度为g)( )| A、金属棒产生的最大感应电动势为Bdv0 | ||||
B、通过金属棒的电荷量为
| ||||
C、克服安培力所做的功为
| ||||
D、整个过程电路中产生的焦耳热为
|
分析:金属棒进入磁场中做减速运动,产生的感应电动势减小,所以开始进入磁场时的感应电动势最大,由公式E=BLv求解最大感应电动势;根据法拉第电磁感应定律、欧姆定律求解感应电荷量;克服安培力所做的功等于电路中产生的焦耳热,根据能量守恒求解.
解答:解:
A、金属棒刚开始进入磁场时产生的感应电动势最大,为 Em=BLv0.故A错误.
B、根据法拉第电磁感应定律得:
=
由欧姆定律得:
=
通过金属棒的电荷量为 q=
△t
磁通量的变化量为△Φ=BLd
联立得:q=
,故B错误.
C、D:根据功能关系得知:克服安培力所做的功等于电路中产生的焦耳热,根据能量守恒得:W=Q=
m
-mgh,故C错误,D正确.
故选:D
A、金属棒刚开始进入磁场时产生的感应电动势最大,为 Em=BLv0.故A错误.
B、根据法拉第电磁感应定律得:
. |
| E |
| △Φ |
| △t |
由欧姆定律得:
. |
| I |
| ||
| 2R |
通过金属棒的电荷量为 q=
. |
| I |
磁通量的变化量为△Φ=BLd
联立得:q=
| BdL |
| 2R |
C、D:根据功能关系得知:克服安培力所做的功等于电路中产生的焦耳热,根据能量守恒得:W=Q=
| 1 |
| 2 |
| v | 2 0 |
故选:D
点评:推导感应电荷量的表达式q=
是解决本题的关键,同时要正确分析能量如何转化的,知道克服安培力所做的功等于电路中产生的焦耳热,这些都是电磁感应问题的基本思路.
| BdL |
| 2R |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目