题目内容
【题目】如图所示传送带A、B之间的距离为L=5．25m，与水平面间夹角
=30o，传送带沿顺时针方向转动，速度恒为v=7．5m/s．在上端A点无初速放置一个质量为m=lkg、大小可视为质点的金属块，它与传送带的动摩擦因数为
，金属块滑离传送带后，沿着弯道滑下，进入半径为R="1" m的光滑半圆轨道做圆周运动，刚好能通过最高点E，D为半圆轨道的最低点且DE垂直于水平面，已知B、D两点的竖直高度差为h=0．5m（取g=10m/s2）．求：
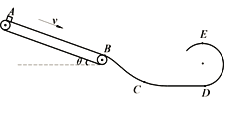
（1）金属块从A运动到B经历的时间
（2）金属块经过半圆轨道的D点时对轨道的压力
（3）金属块在BCD弯道上克服摩擦力做的功。
【答案】（1）1s（2）60N（3）
【解析】试题分析：（1）物体速度到达v的过程中由牛顿第二定律可知
解得
需要的时间
通地过的位移
因为
且
，物体将匀速运动
匀速运动时间
（2）物体刚好通过E点，则
物体从D到E过程中由动能定理可知
在D点由牛顿第二定律可知
联立解得
由牛顿第三定律可知对轨道压力为60N
（3）在BCD过程中有动能定理可得
代入数据解得
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某同学探究弹力与弹簧伸长量的关系．
（1）将弹簧悬挂在铁架台上，将刻度尺固定在弹簧一侧．弹簧轴线和刻度尺都应在__方向（填“水平”或“竖直”）．
（2）弹簧自然悬挂，待弹簧_____时，长度记为L0；弹簧下端挂上砝码盘时，长度记为Lx；在砝码盘中每次增加10 g砝码，弹簧长度依次记为L1至L6，数据如下表．
代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
数值（cm） | 25．35 | 27．35 | 29．35 | 31．30 | 33．4 | 35．35 | 37．40 | 39．30 |
（3）如图是该同学根据表中数据作的图，纵轴是砝码的质量，横轴是弹簧长度与_____的差值（填“L0”或“Lx”）．
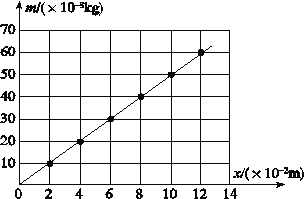
（4）由图可知弹簧的劲度系数为________ N/m；通过图和表可知砝码盘的质量为_______g．（结果保留两位有效数字，重力加速度取9．8 m/s2）
