题目内容
如图16-18所示,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为l.d=0时,磁场的磁感应强度B从B0开始均匀增大,同时,在板2的左端且非常靠近板2的位置有一质量为m、带电荷量为-q的液滴以初速度v0水平向右射入两板间,该液滴可视为质点.

图16-18
(1)要使该液滴能从两板间射出,磁感应强度随时间的变化率k应满足什么条件?
(2)要使该液滴能从板间右端的中点射出,磁感应强度B与时间t应满足什么关系?
(1) ![]() (2)B=B0+
(2)B=B0+![]()
解析:
(1)由题意可知:板1为正极板,2为负极,两板间电压U=![]() =Sk ①
=Sk ①
而S=πr2 ②
带电液滴受电场力:
F=qE=![]() ③
③
故:F-mg=![]() -mg=ma
-mg=ma
所以a=![]() -g ④
-g ④
讨论:
Ⅰ.若a>0,则液滴向上偏转,做类平抛运动
y=![]() ⑤
⑤
当液滴刚好能射出时:
有l=v0t,t=![]() ,y=d
,y=d
故d=![]() ⑥
⑥
由①②⑥得:k1=![]() ⑦
⑦
要使液滴能射出,必须满足y<d,故k<k1.
Ⅱ.若a=0,液滴不发生偏转,做匀速直线运动,此时
a=![]() -g=0 ⑧
-g=0 ⑧
由①②⑧得k2=![]()
液滴能射出必须满足k=k2.
Ⅲ.若a<0,液滴将被吸附在板2上.
综上所述:液滴能射出,k应满足
![]() .
.
(2)B=B0+kt
当液滴从两板间中点射出时,满足条件Ⅰ的情况,则用![]() 替换⑦式中的d
替换⑦式中的d
k=![]()
即B=B0+![]() .
.


 C,质量
C,质量 kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。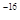 J,求加速电压
J,求加速电压 =1.6×10
=1.6×10 C,质量
C,质量 =0.91×10
=0.91×10 kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
 J,求加速电压
J,求加速电压 为多大;
为多大; =4.0cm,两板间距离
=4.0cm,两板间距离 =1.0cm,极板右端与荧光屏的距离
=1.0cm,极板右端与荧光屏的距离 =18cm,当在偏转电极上加
=18cm,当在偏转电极上加 的正弦交变电压时,如果电子进入偏转电场的初速度
的正弦交变电压时,如果电子进入偏转电场的初速度 ,求电子打在荧光屏上产生亮线的最大长度;
,求电子打在荧光屏上产生亮线的最大长度; 、
、 和
和 三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图14丁所示的电场,图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。
三个阳极除了对电子加速外,还共同完成对电子的聚焦作用,其中聚焦电场可简化为如图14丁所示的电场,图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。