题目内容
1.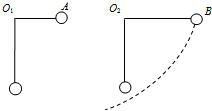 如图所示,原长为L1的橡皮条和长为L2的细线固定在同一水平线上的O1、O2两点,L1<L2.橡皮条和细线的另一端分别拴着质量相同的小球A和B,将两者都拉至水平由静止释放,摆至最低点时,橡皮条和细线的长度恰好相等,则两小球在最低点时速度大小vA与vB相比较( )
如图所示,原长为L1的橡皮条和长为L2的细线固定在同一水平线上的O1、O2两点,L1<L2.橡皮条和细线的另一端分别拴着质量相同的小球A和B,将两者都拉至水平由静止释放,摆至最低点时,橡皮条和细线的长度恰好相等,则两小球在最低点时速度大小vA与vB相比较( )| A. | vA>vB | B. | vA=vB | C. | vA<vB | D. | 无法确定 |
分析 对A球,重力势能的减小量等于动能的增加量和弹性势能的增加量,对于B球,重力势能的减小量等于动能的增加量,根据能量守恒定律求出小球到达最低点的速度,从而比较大小.
解答 解:对A球,重力势能的减小量等于动能的增加量和弹性势能的增加量,根据能量守恒定律得,$mg{l}_{2}=\frac{1}{2}m{{v}_{A}}^{2}+{E}_{P}$
对于B球,重力势能的减小量等于动能的增加量,根据能量守恒有:$mg{l}_{2}=\frac{1}{2}m{{v}_{B}}^{2}$
重力势能减小相同,所以B球的动能大于A球的动能,因为质量相等,所以B球的速度较大.故C正确,A、B、D错误.
故选:C
点评 解决本题的关键知道A球重力势能的减小量等于弹性势能和动能增加量之和,B球重力势能的减小量等于动能的增加量.

练习册系列答案
相关题目
7. 某同学在竖直悬挂的弹簧下面加挂钩码,通过实验研究弹力与弹簧伸长的关系,下表是他的实验数据.实验时弹簧始终未超出弹性限度,弹簧很轻(自身重力可以忽略不计),取g=10m/s2.
某同学在竖直悬挂的弹簧下面加挂钩码,通过实验研究弹力与弹簧伸长的关系,下表是他的实验数据.实验时弹簧始终未超出弹性限度,弹簧很轻(自身重力可以忽略不计),取g=10m/s2.
(1)根据实验数据在坐标纸上作出弹力F和弹簧长度l关系的图象;
(2)根据图象可知:弹簧的劲度系数k=20N/m,弹簧的原长l0=5cm.
 某同学在竖直悬挂的弹簧下面加挂钩码,通过实验研究弹力与弹簧伸长的关系,下表是他的实验数据.实验时弹簧始终未超出弹性限度,弹簧很轻(自身重力可以忽略不计),取g=10m/s2.
某同学在竖直悬挂的弹簧下面加挂钩码,通过实验研究弹力与弹簧伸长的关系,下表是他的实验数据.实验时弹簧始终未超出弹性限度,弹簧很轻(自身重力可以忽略不计),取g=10m/s2.(1)根据实验数据在坐标纸上作出弹力F和弹簧长度l关系的图象;
| 钩码质量m/g | 20 | 40 | 60 | 80 | 100 | 120 |
| 弹簧总长度l/cm | 6.0 | 7.0 | 8.0 | 9.0 | 9.8 | 11.0 |
9. 如图所示为多用电表电阻挡的原理图,表头内阻为Rg,调零电阻为R0,电池的电动势为E,内阻为r,则下列说法中正确的是( )
如图所示为多用电表电阻挡的原理图,表头内阻为Rg,调零电阻为R0,电池的电动势为E,内阻为r,则下列说法中正确的是( )
 如图所示为多用电表电阻挡的原理图,表头内阻为Rg,调零电阻为R0,电池的电动势为E,内阻为r,则下列说法中正确的是( )
如图所示为多用电表电阻挡的原理图,表头内阻为Rg,调零电阻为R0,电池的电动势为E,内阻为r,则下列说法中正确的是( )| A. | 它是根据闭合电路欧姆定律制成的 | |
| B. | 电阻挡对应的“∞”刻度一般在刻度盘的右端 | |
| C. | 接表内电池负极的应是红表笔 | |
| D. | 调零后刻度盘的中心刻度值是r+Rg+R |
13. 有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(阻值可随压力大小而变化的电阻器)、显示体重的仪表?(实质是理想电流表),设踏板的质量可忽略不计,已知仪表?的量程为3A,电源电动势为12V,内阻为2Ω,压力传感器R的阻值随压力变化的函数式为R=30-0.02F(F和R的单位分别是N和Ω).下列说法正确的是( )
有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(阻值可随压力大小而变化的电阻器)、显示体重的仪表?(实质是理想电流表),设踏板的质量可忽略不计,已知仪表?的量程为3A,电源电动势为12V,内阻为2Ω,压力传感器R的阻值随压力变化的函数式为R=30-0.02F(F和R的单位分别是N和Ω).下列说法正确的是( )
 有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(阻值可随压力大小而变化的电阻器)、显示体重的仪表?(实质是理想电流表),设踏板的质量可忽略不计,已知仪表?的量程为3A,电源电动势为12V,内阻为2Ω,压力传感器R的阻值随压力变化的函数式为R=30-0.02F(F和R的单位分别是N和Ω).下列说法正确的是( )
有一种测量人体重的电子秤,其原理图如图所示,它主要由三部分构成:踏板、压力传感器R(阻值可随压力大小而变化的电阻器)、显示体重的仪表?(实质是理想电流表),设踏板的质量可忽略不计,已知仪表?的量程为3A,电源电动势为12V,内阻为2Ω,压力传感器R的阻值随压力变化的函数式为R=30-0.02F(F和R的单位分别是N和Ω).下列说法正确的是( )| A. | 该秤能测量的最大体重是1400N | |
| B. | 该秤零刻度线应标在仪表?刻度盘的最右端 | |
| C. | 体重为1300N应标在仪表?刻度盘2A刻度处 | |
| D. | 该秤零刻度线(即踏板空载时的刻度线)应标在仪表?刻度盘零刻度处 |
10. 如图所示,两根直木棍相互平行,斜靠在竖直墙壁上固定不动,一根水泥圆筒从木棍的上部匀速滑下.若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将水泥圆筒放在两木棍上部,则水泥圆筒在两木棍上受到木棍的摩擦力与原来相比( )
如图所示,两根直木棍相互平行,斜靠在竖直墙壁上固定不动,一根水泥圆筒从木棍的上部匀速滑下.若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将水泥圆筒放在两木棍上部,则水泥圆筒在两木棍上受到木棍的摩擦力与原来相比( )
 如图所示,两根直木棍相互平行,斜靠在竖直墙壁上固定不动,一根水泥圆筒从木棍的上部匀速滑下.若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将水泥圆筒放在两木棍上部,则水泥圆筒在两木棍上受到木棍的摩擦力与原来相比( )
如图所示,两根直木棍相互平行,斜靠在竖直墙壁上固定不动,一根水泥圆筒从木棍的上部匀速滑下.若保持两木棍倾角不变,将两棍间的距离减小后固定不动,仍将水泥圆筒放在两木棍上部,则水泥圆筒在两木棍上受到木棍的摩擦力与原来相比( )| A. | 增大 | B. | 减少 | ||
| C. | 不变 | D. | 条件不足,不能判定 |
11.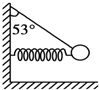 细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连.平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos 53°=0.6,sin 53°=0.8)以下说法正确的是( )
细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连.平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos 53°=0.6,sin 53°=0.8)以下说法正确的是( )
 细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连.平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos 53°=0.6,sin 53°=0.8)以下说法正确的是( )
细绳拴一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连.平衡时细绳与竖直方向的夹角为53°,如图所示.(已知cos 53°=0.6,sin 53°=0.8)以下说法正确的是( )| A. | 弹簧的弹力大小为$\frac{3}{5}$mg | B. | 细绳的拉力大小为$\frac{3}{5}$mg | ||
| C. | 弹簧的弹力大小为$\frac{5}{3}$mg | D. | 细绳的拉力大小为$\frac{5}{3}$mg |
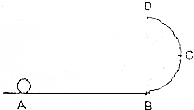 如图所示,固定的光滑水平轨道与半径为R的光滑竖直半圆轨道BCD平滑相接,轨道皆绝缘,B、D为最低点和最高点,C与圆心等高,B、C、D处设有开关,可改变电场方向.有一质量为m、带电量为+q的小球,在水平轨道上的A点由静止释放,起初空间有水平向右的匀强电场,场强E=$\frac{mg}{q}$,当小球运动通过每一个开关时电场将保持场强大小不变,而方向向逆时针旋转90°.
如图所示,固定的光滑水平轨道与半径为R的光滑竖直半圆轨道BCD平滑相接,轨道皆绝缘,B、D为最低点和最高点,C与圆心等高,B、C、D处设有开关,可改变电场方向.有一质量为m、带电量为+q的小球,在水平轨道上的A点由静止释放,起初空间有水平向右的匀强电场,场强E=$\frac{mg}{q}$,当小球运动通过每一个开关时电场将保持场强大小不变,而方向向逆时针旋转90°. (1)用50分度的游际卡尺测量金属管的内径,示数如图乙所示,金属管的内径为d=1.12cm;
(1)用50分度的游际卡尺测量金属管的内径,示数如图乙所示,金属管的内径为d=1.12cm; 有一种测温装置如图所示,玻璃泡A内封有一定量气体,与A相连的B管插在水银槽中,管内水银面的高度x即可反应泡内气体的温度,即环境温度,并可由管B管上的刻度直接读出.设B管的体积与A泡的体积相比可忽略不计.在标准大气压下对B管进行温度刻度(一标准大气压相当于76cmHg的压强).已知当温度t1=27℃时,管内水银面高度x1=16cm,此高度即为27℃的刻度线.问当温度t=0℃的刻度线在x为多少厘米处?
有一种测温装置如图所示,玻璃泡A内封有一定量气体,与A相连的B管插在水银槽中,管内水银面的高度x即可反应泡内气体的温度,即环境温度,并可由管B管上的刻度直接读出.设B管的体积与A泡的体积相比可忽略不计.在标准大气压下对B管进行温度刻度(一标准大气压相当于76cmHg的压强).已知当温度t1=27℃时,管内水银面高度x1=16cm,此高度即为27℃的刻度线.问当温度t=0℃的刻度线在x为多少厘米处?