题目内容
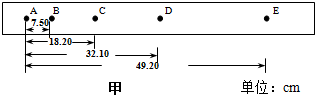
7.如甲图所示为某一同学一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的记数点,相邻记数点间有4个记数点未标出,设A点为计时起点(电源频率为50Hz)(1)由图判断小车做匀加速直线运动
(2)相邻两记数点间的时间间隔为0.1s
(3)BE间的平均速度为1.39 m/s
(4)C点的瞬时速度为1.23m/s
(5)小车的加速度a=3.20m/s2
(6)如果当时交变电流的频率是f=49Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比偏大(选填“偏大”、“偏小”或“不变”)
分析 根据连续相等时间内的位移之差是否为一恒量判断小车的运动规律.根据打点的周期得出相邻计数点间的时间间隔.
根据平均速度的定义式求出BE间的平均速度,结合某段时间内的平均速度等于中间时刻的瞬时速度求出C点的瞬时速度.
根据连续相等时间内的位移之差是一恒量求出加速度,结合打点的周期的测量误差,根据△x=aT2判断加速度的测量误差.
解答 解:(1)由图可知xAB=7.50cm、xBC=10.70cm、xCD=13.90cm、xDE=17.10cm,可知连续相等时间内的位移之差是一恒量,则小车做匀加速直线运动.
(2)打点的周期为0.02s,相邻记数点间有4个点未标出,则相邻计数点间的时间间隔为0.1s.
(3)BE间的平均速度$\overline{v}=\frac{{x}_{BE}}{3T}=\frac{0.492-0.075}{0.3}m/s$=1.39m/s.
(4)C点的瞬时速度等于BD间的平均速度,则${v}_{C}=\frac{{x}_{BD}}{2T}=\frac{0.321-0.075}{0.2}$m/s=1.23m/s.
(5)因为连续相等时间内的位移之差△x=3.20cm,根据△x=aT2得,加速度a=$\frac{△x}{{T}^{2}}=\frac{3.20×1{0}^{-2}}{0.01}m/{s}^{2}=3.20m/{s}^{2}$.
(6)当时交变电流的频率是f=49Hz,而做实验的同学并不知道,周期的测量值为0.02s,可知周期的测量值偏小,根据a=$\frac{△x}{{T}^{2}}$知,加速度的测量值偏大.
故答案为:(1)匀加速直线,(2)0.1,(3)1.39,(4)1.23,(5)3.20.(6)偏大.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

| A. | 在验证力的平行四边形定则实验,同一次实验两次拉细绳套须使结点到达同一位置,运用了等效替代法 | |
| B. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| C. | 在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,该实验应用了控制变量法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
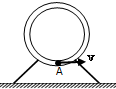 如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )
如图所示,质量为M=1kg的薄壁细圆管竖直放置在固定的底座上,圆管内部光滑,圆半径比细管的内径大得多.已知圆的半径R=0.4m,一质量m=0.5kg的小球,在管内最低点A的速度大小为$2\sqrt{2}$m/s,g取10m/s2,则以下说法正确的是( )| A. | 小球恰能做完整的圆周运动 | |
| B. | 小球沿圆轨道上升的最大高度为0.4m | |
| C. | 圆管对底座的最大压力为15N | |
| D. | 圆管对底座的最大压力等于25N |
| A. | 加速度增大,速度一定增大 | |
| B. | 速度变化量△v大,加速度一定大 | |
| C. | 速度变化越来越快,加速度越来越大 | |
| D. | 物体速度很大,加速度可以为零 |
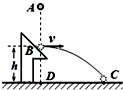 如图所示,从A点由静止释放一小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同时间落于地上C点,已知地面上D点位于B点正下方,B、D间距离为h,则( )
如图所示,从A点由静止释放一小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同时间落于地上C点,已知地面上D点位于B点正下方,B、D间距离为h,则( )| A. | AB两点间距离为h | B. | AB两点间距离为$\frac{h}{2}$ | ||
| C. | CD两点间距离为2h | D. | CD两点间距离为$\sqrt{2}$h |
| A. | F1与车前进方向相反 | B. | F2与车前进方向相同 | ||
| C. | F3与车前进方向相反 | D. | F4与车前进方向相同 |

 现有一合金制成的圆柱体.为测量该合金的电阻率,现用伏安法测量圆柱体两端之间的电阻,用螺旋测微器测量该圆柱体的直径示数如图,读数为1.842mm.若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的直径和长度分别用D、L表示,则用D、L、I、U表示的电阻率的关系式为ρ=$\frac{πU{D}^{2}}{4IL}$.
现有一合金制成的圆柱体.为测量该合金的电阻率,现用伏安法测量圆柱体两端之间的电阻,用螺旋测微器测量该圆柱体的直径示数如图,读数为1.842mm.若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的直径和长度分别用D、L表示,则用D、L、I、U表示的电阻率的关系式为ρ=$\frac{πU{D}^{2}}{4IL}$.