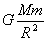题目内容
2003年2月1日，美国哥伦比亚号航天飞机在返回途中解体，成为人类航天史上的一大悲剧．若哥伦比亚号航天飞机是在赤道上空飞行，轨道半径为r，飞行方向与地球自转方向相同，设地球自转角速度为ω0，地球半径为R，地球表面重力加速度为g，在某时刻航天飞机通过赤道上某建筑物上方，则到它下次通过该建筑上方所需时间为（ ）
分析：根据人造卫星的万有引力等于向心力，列式求出角速度的表达式，卫星再次经过某建筑物的上空，比地球多转动一圈．
解答：解：人造卫星绕地球做匀速圆周运动，根据万有引力提供向心力，设卫星的质量为m、轨道半径为r、地球质量为M，有：
F=
=mω2r
解得ω=
①
卫星再次经过某建筑物的上空，卫星多转动一圈，有：
（ω-ω0）t=2π ②
在地球表面，重力等于万有引力得：
=mg
地球表面的重力加速度为：g=
③
联立①②③后，解得：
t=
故选：D．
F=
| GMm |
| r2 |
解得ω=
|
卫星再次经过某建筑物的上空，卫星多转动一圈，有：
（ω-ω0）t=2π ②
在地球表面，重力等于万有引力得：
| GMm |
| R2 |
地球表面的重力加速度为：g=
| GM |
| R2 |
联立①②③后，解得：
t=
| 2π | ||||
|
故选：D．
点评：本题关键：（1）根据万有引力提供向心力求解出角速度；（2）根据地球表面重力等于万有引力得到重力加速度表达式；（3）根据多转动一圈后再次到达某建筑物上空列式．
练习册系列答案
相关题目
-ω0) B.2π(
+
)
D.2π/(
+ω0)
B.2π
D.2π/