题目内容
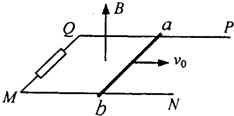
 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为M,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.求在此过程中:
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为M,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.求在此过程中:(1)流过电阻R的电流方向?
(2)电阻R上产生的焦耳热QJ=?
(3)通过电阻R的总电量q=?
分析:(1)流过电阻R的电流方向由右手定则判断;
(2)导体棒ab向右运动,切割感应磁感线产生感应电流,棒ab将受到向左的安培力作用而做减速运动,最终棒ab停止运动,其初动能全部转化为内能,根据能量守恒列式求解焦耳热.
(3)对于ab棒,运用动量定理列式求解通过电阻R的总电量q.
(2)导体棒ab向右运动,切割感应磁感线产生感应电流,棒ab将受到向左的安培力作用而做减速运动,最终棒ab停止运动,其初动能全部转化为内能,根据能量守恒列式求解焦耳热.
(3)对于ab棒,运用动量定理列式求解通过电阻R的总电量q.
解答:解:(1)根据右手定则判断可知,流过电阻R的电流方向:M→Q;
(2)ab棒向右运动的过程中,受到向左的安培力作用,做减速运动,最终棒ab停止运动,其初动能
m
全部转化为内能,则根据能量守恒定律得:
电阻R上产生的焦耳热QJ=
m
;
(3)设ab滑行过程中,通过的感应电流平均值为
,运动时间为t,取向右方向为正方向,则对ab棒,由动量定理得:
-B
Lt=-mv0,
又通过R的总电量 q=
t
联立解得,q=
答:(1)流过电阻R的电流方向为M→Q;(2)电阻R上产生的焦耳热QJ=
m
;(3)通过电阻R的总电量q=
.
(2)ab棒向右运动的过程中,受到向左的安培力作用,做减速运动,最终棒ab停止运动,其初动能
| 1 |
| 2 |
| v | 2 0 |
电阻R上产生的焦耳热QJ=
| 1 |
| 2 |
| v | 2 0 |
(3)设ab滑行过程中,通过的感应电流平均值为
. |
| I |
-B
. |
| I |
又通过R的总电量 q=
. |
| I |
联立解得,q=
| mv0 |
| BL |
答:(1)流过电阻R的电流方向为M→Q;(2)电阻R上产生的焦耳热QJ=
| 1 |
| 2 |
| v | 2 0 |
| mv0 |
| BL |
点评:由能量守恒求电阻产生的焦耳热比较容易,关键是针对变减速运动过程,能够运用动量定理求解电量,这种方法比较特殊,通过训练,提高这方面的解题能力.

练习册系列答案
相关题目
 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )| A、电阻R上产生的焦耳热 | B、通过电阻R的总电荷量 | C、ab棒运动的位移 | D、ab棒运动的时间 |
 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为M,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上,则在此过程中整个回路产生的焦耳热为
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为M,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上,则在此过程中整个回路产生的焦耳热为 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中可求出的物理量有( )