Question

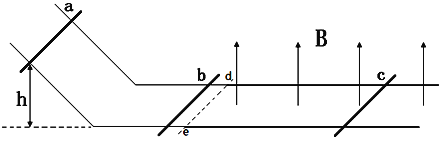
【题目】如图所示，平行倾斜光滑导轨与足够长的平行水平光滑导轨平滑连接，导轨电阻不计。质量分别为和的金属棒b和c静止放在水平导轨上，b、c两棒均与导轨垂直。图中de虚线以右有范围足够大、方向竖直向上的匀强磁场。质量为的绝缘棒a垂直于倾斜导轨静止释放，释放位置与水平导轨的高度差为h。已知绝缘棒a滑到水平导轨上与金属棒b发生弹性正碰，金属棒b进入磁场后始终未与金属棒c发生碰撞。重力加速度为g。

求：（1）绝缘棒a与金属棒b发生弹性正碰后分离时两棒的速度；

（2）两金属棒b、c上最终产生的总焦耳热；

（3）求金属棒b进入磁场后，其加速度为其最大加速度的一半时的速度。

Answer 1

【答案】（1）（2）（3）

【解析】试题分析：（1）a棒沿着斜面下滑过程只有重力做功，根据机械能守恒定律列式求出a棒滑到斜面底端时的速度；棒a与金属棒b发生弹性正碰，根据动量守恒定律和机械能守恒定律列式，可求得分离时两棒的速度；（2）b棒获得速度后向右做切割磁感线运动，产生感应电流，在安培力作用下，b棒做减速运动，c棒做加速运动，最终bc两棒以相同的速度匀速运动，由于系统的合外力为零，遵守动量守恒定律根据动量守恒定律列式求解共同速度，然后结合功能关系求解产生的总焦耳热；（3）b棒刚进磁场的加速度最大．当b棒加速度为最大值的一半时，根据系统的动量守恒和速度关系求解．

（1）a棒沿着斜面下滑的过程机械能守恒，则有

a棒与b棒发生弹性碰撞，取向右为正方向，由动量守恒定律得
根据机械能守恒有

解出碰后a、b两棒的速度分别为

（2）最终b、c以相同的速度匀速运动．设共同速度为v．取向右为正方向，根据动量守恒定律得

由能量守恒得

解出

（3）b棒刚进磁场的加速度最大．由动量守恒得

根据，

知当b棒加速度为最大值的一半时有

联立得