题目内容
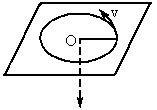
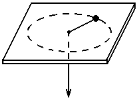 小球被绳子牵引在光滑水平的板上做匀速圆周运动,其半径R=30cm,速率v=1.0m/s,现牵引的绳子迅速放长20cm,使小球在更大半径的新轨道上做匀速圆周运动.绳子绷紧瞬间沿绳方向的速度突变为零.
小球被绳子牵引在光滑水平的板上做匀速圆周运动,其半径R=30cm,速率v=1.0m/s,现牵引的绳子迅速放长20cm,使小球在更大半径的新轨道上做匀速圆周运动.绳子绷紧瞬间沿绳方向的速度突变为零.求(1)实现这一过渡所经历的时间
(2)新轨道上小球的角速度是多少?
分析:放长绳子后,小球先做匀速直线运动,根据勾股定理列方程求小球的位移;小球在新轨道上做匀速圆周运动的线速度为原速度在垂直绳子方向上的分量,从而求出新轨道上的线速度,然后根据公式v=ωr求解角速度.
解答:解:(1)放长绳子后,小球先做匀速直线运动,如图所示,设小球的位移为x,有:
x2+R2=(R+0.2)2
解得:x=0.4m
则t=
=0.4s

(2)小球在新轨道上做匀速圆周运动的线速度为v′,

绳子伸长被拉直后只保留垂直于绳子方向的分速度:v′=v?cos53°=0.6m/s
ω=
=1.2rad/s
答:(1)实现这一过渡所经历的时间为0.4s
(2)新轨道上小球的角速度是多少1.2rad/s
x2+R2=(R+0.2)2
解得:x=0.4m
则t=
| x |
| v |

(2)小球在新轨道上做匀速圆周运动的线速度为v′,

绳子伸长被拉直后只保留垂直于绳子方向的分速度:v′=v?cos53°=0.6m/s
ω=
| v |
| r |
答:(1)实现这一过渡所经历的时间为0.4s
(2)新轨道上小球的角速度是多少1.2rad/s
点评:小球先做匀速直线运动;小球在新轨道上做匀速圆周运动的线速度为v′为原速度在垂直于绳子方向上的分量,画出图后不难求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
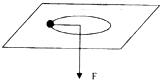 如图所示,一个被绳子牵引的小球在光滑水平板上以速度v=1.0m/s做匀速圆周运动.运动半径r=30cm.现迅速松手使绳子放长20cm后立即拽紧绳子,使小球在更大半径的新轨道上做匀速圆周运动.
如图所示,一个被绳子牵引的小球在光滑水平板上以速度v=1.0m/s做匀速圆周运动.运动半径r=30cm.现迅速松手使绳子放长20cm后立即拽紧绳子,使小球在更大半径的新轨道上做匀速圆周运动.