题目内容
13. 把一带电量为+q质量为m的小球放在倾角为30°的光滑绝缘斜面上的D点,已知BD间距离为r,BD⊥MD.欲使小球能静止在斜面上
把一带电量为+q质量为m的小球放在倾角为30°的光滑绝缘斜面上的D点,已知BD间距离为r,BD⊥MD.欲使小球能静止在斜面上(1)若在MB的中点A处放一个点电荷,则该电荷的电量$\frac{\sqrt{3}mg{r}^{2}}{3k{q}_{1}}$
(2)若加匀强电场且场强值最小,则该电场强度的方向为$\frac{mg}{2q}$.
分析 (1)对点电荷受力分析,根据共点力平衡即可求得在A点施加的电荷量
(2)小球的重力沿斜面向下的分力mgsinα一定,当电场力沿斜面向上时,电场力最小,电场强度最小.由平衡条件求解
解答 解:(1)对电荷受力分析如图, 根据共点力平衡可知$\frac{k{q}_{1}q}{{r}^{2}}cos30°=mgsin30°$
根据共点力平衡可知$\frac{k{q}_{1}q}{{r}^{2}}cos30°=mgsin30°$
解得q=$\frac{\sqrt{3}mg{r}^{2}}{3k{q}_{1}}$
(2)小球的重力沿斜面向下的分力mgsinα一定,当电场力沿斜面向上时,电场力最小,电场强度最小.此时电场强度方向沿斜面向上.
由平衡条件得:mgsinθ=QE,则电场强度的最小值 E=$\frac{mgsin30°}{q}=\frac{mg}{2q}$
故答案为:$\frac{\sqrt{3}mg{r}^{2}}{3k{q}_{1}}$,$\frac{mg}{2q}$
点评 本题是通电导体在电场中平衡问题类型,关键是分析电场力的大小和方向

练习册系列答案
相关题目
3.用m表示地球通讯卫星的质量,h表示它离地面的高度,R0表示地球的半径,g0表示地球表面处的重力加速度,ω0表示地球自转的角速度,则通讯卫星所受地球对它的万有引力的大小为( )
| A. | 0 | B. | mω02(R0+h) | C. | $\frac{m{{R}_{0}}^{2}{g}_{0}}{({R}_{0}+h)^{2}}$ | D. | m$\root{3}{{{R}_{0}}^{2}{g}_{0}{{ω}_{0}}^{4}}$ |
4.下列哪种措施不是利用良好接地来防范静电的危害的( )
| A. | 飞机的轮子用导电橡胶做成 | B. | 油罐车的上拖一条铁链到地上 | ||
| C. | 印染厂里需要增加空气的湿度 | D. | 高楼大厦上使用避雷针 |
1.关于库仑定律$F=k\frac{{{q_1}{q_2}}}{r^2}$,下列说法中正确的是( )
| A. | 库仑定律是实验定律 | |
| B. | 可以用来计算任何带电体之间的相互作用力大小 | |
| C. | 当r→0时,电荷之间的库仑力趋向于无穷大 | |
| D. | k叫静电力常量,其数值为k=1.6×10-19N•m2/C2 |
8.如图所示,在静电场中,一个负电荷q受到一个非静电力作用,由A点移到B点,则以下说法正确的是( )
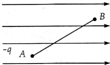

| A. | 非静电力和电场力做功之和等于电荷电势能增量和动能增量之和 | |
| B. | 非静电力做功和电场力做功之和等于电荷动能的增量 | |
| C. | 电荷克服电场力做功等于电势能的增量 | |
| D. | 非静电力做功等于电势能增量和动能增量之和 |
18. 如图,一个枕形导体AB原来不带电.将它放在一个负点电荷的电场中,点电荷的电量为Q,与AB中心O点的距离为R.由于静电感应,在导体A、B两端分别出现感应电荷.当达到静电平衡时( )
如图,一个枕形导体AB原来不带电.将它放在一个负点电荷的电场中,点电荷的电量为Q,与AB中心O点的距离为R.由于静电感应,在导体A、B两端分别出现感应电荷.当达到静电平衡时( )
 如图,一个枕形导体AB原来不带电.将它放在一个负点电荷的电场中,点电荷的电量为Q,与AB中心O点的距离为R.由于静电感应,在导体A、B两端分别出现感应电荷.当达到静电平衡时( )
如图,一个枕形导体AB原来不带电.将它放在一个负点电荷的电场中,点电荷的电量为Q,与AB中心O点的距离为R.由于静电感应,在导体A、B两端分别出现感应电荷.当达到静电平衡时( )| A. | 导体A端电势高于B端电势 | B. | 导体A端电势低于B端电势 | ||
| C. | 导体中心O点的场强为0 | D. | 导体中心O点的场强为$\frac{kQ}{{R}^{2}}$ |
2.高速行驶的竞赛汽车依靠摩擦力转弯是有困难的,所以竞赛场地的弯道处做成斜坡,如果弯道半径为r,斜坡和水平方向成θ角,则汽车完全不依靠摩擦力转弯的速度大小为( )
| A. | $\sqrt{grsinθ}$ | B. | $\sqrt{grcosθ}$ | C. | $\sqrt{grtanθ}$ | D. | $\sqrt{grcotθ}$ |
 如图是示波管示意图,竖直偏转电极的极板长l=4cm,板间距离d=1cm,板右端距离荧光屏L=18cm.(水平偏转电极上不加电压,没有画出.)电子沿中心线进入竖直偏转电场的速度是1.6×107m/s.电子电量e=1.60×10-19C,质量m=0.91×10-30 kg.
如图是示波管示意图,竖直偏转电极的极板长l=4cm,板间距离d=1cm,板右端距离荧光屏L=18cm.(水平偏转电极上不加电压,没有画出.)电子沿中心线进入竖直偏转电场的速度是1.6×107m/s.电子电量e=1.60×10-19C,质量m=0.91×10-30 kg.