题目内容
20. 边长为L的正方形线框abcd在磁感应强度为B的匀强磁场中绕轴OO′匀速转动.初始时刻线框平面与磁场垂直,如图所示.经过t时间,线框转过120°.求:
边长为L的正方形线框abcd在磁感应强度为B的匀强磁场中绕轴OO′匀速转动.初始时刻线框平面与磁场垂直,如图所示.经过t时间,线框转过120°.求:(1)线框转动周期和线框转过120°时感应电动势的瞬时值;
(2)若线框电阻为r,小灯泡电阻为R,计算小灯泡的电功率.
分析 电动势的平均值利用公式E=$\frac{△Φ}{△t}$,瞬时值,先求出最大值,再根据瞬时值表达式求转过一定角度时的瞬时值,根据欧姆定律求解灯泡的电功率.
解答 解:(1)整个过程中只有CD边切割磁感线,经过时间t,线框转过1200角,说明周期T=3t,电动势瞬时值为:
E2=NB$\frac{2π}{3t}$L2sin120°
解得:E2=$\frac{\sqrt{3}πB{L}^{2}}{3t}$
(2)电动势的最大值:${E}_{m}=NBSω=\frac{2πB{L}^{2}}{3t}$,
回路中的电流有效值为:$I=\frac{\frac{{E}_{m}}{\sqrt{2}}}{R+r}$
小灯泡的电功率:P=I2R=$\frac{2{π}^{2}{B}^{2}{L}^{4}R}{9(R+r)^{2}{t}^{2}}$
答:(1)线框转动周期和线框转过120°时感应电动势的瞬时值$\frac{\sqrt{3}πB{L}^{2}}{3t}$;
(2)若线框电阻为r,小灯泡电阻为R,计算小灯泡的电功率$\frac{2{π}^{2}{B}^{2}{L}^{4}R}{9(R+r)^{2}{t}^{2}}$.
点评 本题考查了电动势瞬时值和平均值的求法,记住瞬时值表达式的写法;注意求解功率时要用到有效值.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
10. 在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制.如图所示,R1为电阻箱,R2为半导体热敏电阻,C为电容器.已知热敏电阻的阻值随温度的升高而减小,则有( )
在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制.如图所示,R1为电阻箱,R2为半导体热敏电阻,C为电容器.已知热敏电阻的阻值随温度的升高而减小,则有( )
 在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制.如图所示,R1为电阻箱,R2为半导体热敏电阻,C为电容器.已知热敏电阻的阻值随温度的升高而减小,则有( )
在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制.如图所示,R1为电阻箱,R2为半导体热敏电阻,C为电容器.已知热敏电阻的阻值随温度的升高而减小,则有( )| A. | 若R1固定,当环境温度降低时电压表的示数减小 | |
| B. | 若R1固定,当环境温度降低时R1消耗的功率增大 | |
| C. | 若R1固定,当环境温度降低时,电容器C的电荷量减少 | |
| D. | 若R1固定,环境温度不变,当电容器C两极板间的距离增大时极板之间的电场强度减小 |
8. 欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
 欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )| A. | 导线中电流的大小与小磁针转过的角度成正比 | |
| B. | 通电后小磁针静止时N极所指的方向是电流产生磁场的方向 | |
| C. | 若将导线垂直于小磁针放置,则不能完成测量 | |
| D. | 这种方法只能测量电流的大小,不能测量电流的方向 |
15. 2008年4月28日凌晨,山东境内发生两列列车相撞事故,造成了大量人员伤亡和财产损失.引发事故的主要原因是其中一列列车转弯时超速行驶.如图所示,是一种新型高速列车,当它转弯时,车厢会自动倾斜,提供转弯需要的向心力;假设这种新型列车以360km/h的速度在水平面内转弯,弯道半径为1.5km,则质量为75kg的乘客在列车转弯过程中所受到的合外力为( )
2008年4月28日凌晨,山东境内发生两列列车相撞事故,造成了大量人员伤亡和财产损失.引发事故的主要原因是其中一列列车转弯时超速行驶.如图所示,是一种新型高速列车,当它转弯时,车厢会自动倾斜,提供转弯需要的向心力;假设这种新型列车以360km/h的速度在水平面内转弯,弯道半径为1.5km,则质量为75kg的乘客在列车转弯过程中所受到的合外力为( )
 2008年4月28日凌晨,山东境内发生两列列车相撞事故,造成了大量人员伤亡和财产损失.引发事故的主要原因是其中一列列车转弯时超速行驶.如图所示,是一种新型高速列车,当它转弯时,车厢会自动倾斜,提供转弯需要的向心力;假设这种新型列车以360km/h的速度在水平面内转弯,弯道半径为1.5km,则质量为75kg的乘客在列车转弯过程中所受到的合外力为( )
2008年4月28日凌晨,山东境内发生两列列车相撞事故,造成了大量人员伤亡和财产损失.引发事故的主要原因是其中一列列车转弯时超速行驶.如图所示,是一种新型高速列车,当它转弯时,车厢会自动倾斜,提供转弯需要的向心力;假设这种新型列车以360km/h的速度在水平面内转弯,弯道半径为1.5km,则质量为75kg的乘客在列车转弯过程中所受到的合外力为( )| A. | 500 N | B. | 1 000 N | C. | 500$\sqrt{2}$N | D. | 0 |
5.汽车A在红绿灯前停住,绿灯亮起时起动,以0.4m/s2的加速度做匀加速运动,经过30s后以该时刻的速度做匀速直线运动.设在绿灯亮的同时,汽车B以8m/s的速度从A车旁边驶过,且一直以相同的速度做匀速直线运动,运动方向与A车相同,则从绿灯亮时开始( )
| A. | A车在加速过程中与B车相遇? | B. | A、B相遇时速度相同? | ||
| C. | 相遇时A车做匀速运动? | D. | 两车可能再次相遇? |
12.一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度-时间(vx-t)图象和y方向的位移-时间(y-t)图象分别如图乙、丙所示,由此可知( )


| A. | t=0s时,质点的速度大小为12m/s | B. | 质点做加速度恒定的曲线运动 | ||
| C. | 前两秒,质点所受的合力大小为10N | D. | t=1.0s时,质点的速度大小为7m/s |
9.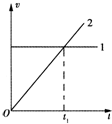 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示,若平抛运动的时间大于2t1,下列说法中正确的是( )| A. | 图线2表示竖直分运动的v-t图线 | |
| B. | t1时刻的速度方向与初速度方向夹角为30° | |
| C. | t1时间内的竖直位移与水平位移之比为$\frac{1}{2}$ | |
| D. | 2t1时刻的速度方向与初速度方向夹角为60° |
10. 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )| A. | $\frac{{{r}_{1}}^{2}{ω}^{2}}{{r}_{3}}$ | B. | $\frac{{{r}_{3}}^{2}{ω}^{2}}{{{r}_{1}}^{2}}$ | C. | $\frac{{{r}_{3}}^{3}{ω}^{2}}{{{r}_{1}}^{2}}$ | D. | $\frac{{r}_{1}{r}_{2}{ω}^{2}}{{r}_{3}}$ |
 如图所示,单摆摆长L=1.0m,C点在悬点O的正下方,D点与C点相距为x=0.6m,C、D之间是光滑绝缘水平面,当摆球A(不带电)运动至左侧最大位移处时,带电小球B从D点由静止释放,小球B的电荷量q=+2.0×10-2C.A、B的质量均为m=200g.当小球B运动到C点时,A、B小球恰在C点迎面相碰.(A、B小球均看成质点,不计空气阻力,计算时取g=10m/s2,π2=10).求
如图所示,单摆摆长L=1.0m,C点在悬点O的正下方,D点与C点相距为x=0.6m,C、D之间是光滑绝缘水平面,当摆球A(不带电)运动至左侧最大位移处时,带电小球B从D点由静止释放,小球B的电荷量q=+2.0×10-2C.A、B的质量均为m=200g.当小球B运动到C点时,A、B小球恰在C点迎面相碰.(A、B小球均看成质点,不计空气阻力,计算时取g=10m/s2,π2=10).求