题目内容
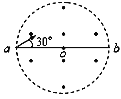
【题目】如图所示，一带正电粒子沿与圆形区域直径ab成30°的方向从a点以速度v0进入匀强磁场，经过t时间从b点离开，已知仅在圆形区域内存在垂直纸面向外的匀强磁场。当粒子调整速度大小后，再次从同一位置以相同的方向进入圆形区域磁场，经过2t时间再次离开圆形区域。则粒子调整后的速度为（粒子重力不计）（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】试题分析：带电粒子在磁场中运动的周期
，与带电粒子的速度和半径无关，所以带电粒子在磁场中运动的时间之比就是它们在磁场中偏转角之比．由于第一次带电粒子偏转60°，则第二次带电粒子在磁场中偏转120°，画出轨迹．从而求出半径与磁场圆半径的关系，从而求出两次带电粒子的速度之比．
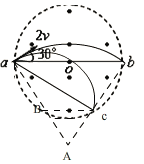
由题设条件画出两种情况下带电粒子的轨迹如图所示，由于是以相同的方向射入的，它们轨迹圆心在以初速度垂直的直线上，如图中的A、B两点，由于速度变化后在磁场中的时间变为2t，则偏转角为120°，即初速度方向与ac成60°，若磁场圆的半径为R，则两种情况下，带电粒子做匀速圆周运动的半径分别为
，由洛仑兹力提供向心力
得到
．所以
，则
，B正确．
练习册系列答案
相关题目
