题目内容
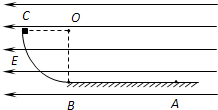 如图所示,BC是半径为R的
如图所示,BC是半径为R的| 1 | 4 |
(1)滑块通过B点时的速度大小Vb?
(2)水平轨道上A、B两点之间的距离S?
(3)从B点运动到A点所用的时间t?
分析:(1)小滑块从C到B的过程中,只有重力和电场力对它做功,根据动能定理求解.
(2)对整个过程研究,重力做正功,水平面上摩擦力做负功,电场力做负功,根据动能定理求出水平轨道上A、B两点之间的距离.
(3)小滑块在水平面上做匀减速运动,末速度为0.
(2)对整个过程研究,重力做正功,水平面上摩擦力做负功,电场力做负功,根据动能定理求出水平轨道上A、B两点之间的距离.
(3)小滑块在水平面上做匀减速运动,末速度为0.
解答:解:(1)小滑块从C到B的过程中,只有重力和电场力对它做功,设滑块通过B点时的速度为vB,根据动能定理有:mgR-qER=
m
解得:vB=
(2)小滑块在AB轨道上运动时,所受摩擦力为f=μmg
小滑块从C经B到A的整个过程中,重力做正功,电场力和摩擦力做负功.设小滑块在水平轨道上运动的距离(即A、B两点间的距离)为L,则根椐动能定理有:
mgR-qE(R+L)-μmgL=0
解得:L=
R
(3)滑块在水平面上做匀减速运动,-μmg-qE=ma
at=0-vB
联立以上2公式解得:t=-
=
答:(1)滑块通过B点时的速度大小为
;
(2)水平轨道上A、B两点之间的距离L=
R.
(3)从B点运动到A点所用的时间
.
| 1 |
| 2 |
| v | 2 B |
解得:vB=
|
(2)小滑块在AB轨道上运动时,所受摩擦力为f=μmg
小滑块从C经B到A的整个过程中,重力做正功,电场力和摩擦力做负功.设小滑块在水平轨道上运动的距离(即A、B两点间的距离)为L,则根椐动能定理有:
mgR-qE(R+L)-μmgL=0
解得:L=
| mg-qE |
| μmg+qE |
(3)滑块在水平面上做匀减速运动,-μmg-qE=ma
at=0-vB
联立以上2公式解得:t=-
| vB |
| a |
| m |
| μmg+qE |
|
答:(1)滑块通过B点时的速度大小为
|
(2)水平轨道上A、B两点之间的距离L=
| mg-qE |
| μmg+qE |
(3)从B点运动到A点所用的时间
| m |
| μmg+qE |
|
点评:本题考查分析和处理物体在复合场运动的能力.对于电场力做功W=qEd,d为两点沿电场线方向的距离.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
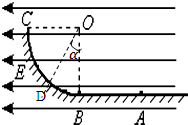 如图所示,BC是半径为R的
如图所示,BC是半径为R的