Question

【题目】如图所示，空间有场强竖直向下的电场，长L=0．8m不可伸长的轻绳固定于O点，另一端系一质量的带电量的小球。拉起小球至绳水平后在A点无初速度释放，当小球运动至O点的正下方B点时绳恰好断裂，小球继续运动并垂直打在同一竖直平面且与水平面成、无限大的挡板MN上的C点，试求：

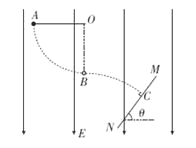
（1）绳子的最大张力

（2）A、C两点的电势差

（3）当小球运动至C点时，突然施加一恒力F作用在小球上，同时把挡板迅速水平向右移至某处，若小球仍能垂直打在挡板上，求所加恒力的最小值。

Answer 1

【答案】（1）30N（2）125V（3）8N

【解析】试题分析：（1）A→B由动能定理及圆周运动知识有： （mg+qE）L＝mvB2…①

T（mg+qE）＝m…②

联解①②得：T=30N…③

（2）A→C由功能关系及电场相关知识有：

（mg+qE）hAC＝mvC2…④

vCsinθ=vB…⑤

UAC=EhAC…⑥

联解④⑤⑥得：UAC=125V…⑦

（3）由题可知施加恒力F后小球必须做匀速直线或匀加速直线运动，才能垂直打在档板上．设恒力F与竖直方向的夹角为α，作出小球的受力矢量三角形分析如图所示．（或由矢量三角形可知：当F与F合（或运动）的方向垂直时，F有最小值而无最大值）…⑧

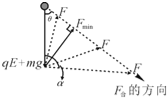
由矢量三角形图有：Fmin=（mg+qE）sinθ…⑨

θ≤（α+θ）≤180°…⑩

联解⑨⑩得：F≥8N…（11）

0°＜α＜127°…（12）