题目内容
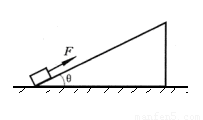
如图所示，在倾角
的足够长的固定斜面底端有一质量m＝1.0 kg的物体．物体与斜面间动摩擦因数μ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10.0 N，方向平行斜面向上．经时间t＝4.0 s绳子突然断了．(g＝10 m/s2)求：
(1)绳断时物体的速度大小．
(2)从绳子断了开始到物体再返回到斜面底端的运动时间？
答案：
解析：
解析：
|
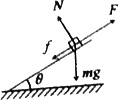
(1)物体受拉力向上运动过程中，受力如下图，根据牛顿第二定律有： 解得 所以绳断时物体的速度大小为
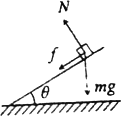
(2)绳断时物体距斜面底端的位移 绳断后物体沿斜面向上运动的过程受力如下图，则根据牛顿第二定律有：
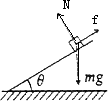
解得 物体做减速运动的时间 减速运动的位移 此后物体将沿斜面匀加速下滑，受力如下图，根据牛顿第二定律有：
解得 物体向下匀加速运动有 解得物体由最高点到斜面底端的时间为t3＝ 所以物体返回到斜面底端的时间为t总＝t2＋t3＝4.2 s 评分标准：本题12分，(1)题3分，(2)题9分．①②③④⑤⑥⑦⑧⑨⑩ |
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
＝3.2 s 
练习册系列答案
快捷英语周周练系列答案
相关题目
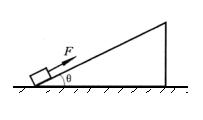
的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数?? ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，(sin37°＝0.60 cos37°＝0.80，g＝10m/s2）
的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数µ ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，(sin37°＝0.60 cos37°＝0.80，g＝10m/s2）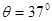
的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数µ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，(sin37°＝0.60 cos37°＝0.80，g＝10m/s2）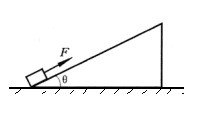
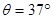的足够长的固定斜面上，物体A和小车B静止在斜面上，A的质量为mA=1.0kg，B的质量为mB=0.5kg，某时刻给物体A一沿斜面A、B两物体在斜面上相遇并发生碰撞，碰撞时间极短且没有机械能损失，已知A与斜端间的动摩擦因数
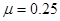，B与斜面间的摩擦不计，取sin37°=0.6，重力加速度g=10m/s2，求
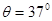的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数µ ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，(sin37°＝0.60 cos37°＝0.80，g＝10m/s2）