��Ŀ����
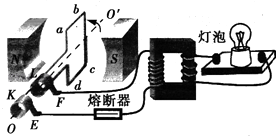
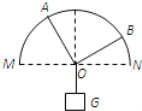
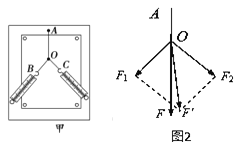
����Ŀ����ͼ��ʾ���⻬б����ˮƽ��ɦ��ǣ�б����һ����Ϊl=0.30m����ˣ�һ��ϵס����Ϊ0.2kg��С����һ�˿���O����б����ת�����Ƚ��������ˮƽλ�ã�Ȼ���С��һ����б�沢����˴�ֱ�ij��ٶ�v0=3m/s��ȡg=10m/s2 �� �� ��
A.��ʱС��ļ��ٶȴ�СΪ ![]() m/s2
m/s2
B.С����ߵ�ʱ���˶���ĵ�����б������
C.������v0 �� С��ﵽ��ߵ�ʱ���Ӷ�С��ĵ���һ������
D.������v0 �� С��ﵽ��ߵ�ʱ���Ӷ�С��ĵ������ܼ�С
���𰸡�B,C
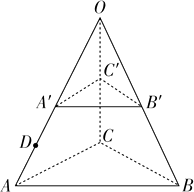
���������⣺A��С��������Բ���˶����ڳ�λ�ü��ٶȲ�ָ��Բ�ģ�����ֽ⣺
������ٶ�Ϊ�� ![]() ��
��
���ļ��ٶ�Ϊ�� ![]()
����ƽ���ı��ζ���֪��С���ʱ�ļ��ٶ�Ϊ��a= ![]() m/s2��A���������⣮
m/s2��A���������⣮
B���ӿ�ʼ����ߵ���̣����ݶ��ܶ������У���mglsin��= ![]() ����ã�v1=
����ã�v1= ![]() �������ٽ���������û�и˵ĵ�����������ƽ��б������ṩ���������У�
�������ٽ���������û�и˵ĵ�����������ƽ��б������ṩ���������У� ![]() �����Եõ�v2С��v1��˵��������ߵ������������B�������⣮
�����Եõ�v2С��v1��˵��������ߵ������������B�������⣮
CD������ߵ�ʱ����˶�С��ĵ������������ʣ�F+mgsin��= ![]() ��������ٶ���������ߵ��ٶ�Ҳ���ӣ�������Fһ�����ӣ�C�������⣬D���������⣮
��������ٶ���������ߵ��ٶ�Ҳ���ӣ�������Fһ�����ӣ�C�������⣬D���������⣮
���Դ��ǣ�BC��
�����㾫�������ڱ��⿼����������Ͷ��ܶ������ۺ�Ӧ�ã���Ҫ�˽�����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ��ܵó���ȷ�𰸣�