题目内容
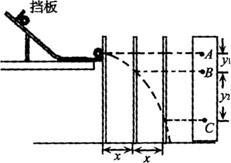
 在“研究平抛物体的运动”的实验中,某同学只记录了A、B、C三点,各点的坐标如图所示,则物体运动的初速度为
在“研究平抛物体的运动”的实验中,某同学只记录了A、B、C三点,各点的坐标如图所示,则物体运动的初速度为1
1
m/s,初始位置的坐标为(-10,-5)
(-10,-5)
(单位为cm,g=10m/s2).分析:平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动.从图中坐标可看出,物体从A→B→C的水平位移一样,都为10cm,设为△x,说明各段的时间相等,设为T,可知△x=v0T,由运动的等时性,T由竖直方向运动求出,从A→B→C的竖直位移依次相差△h=10cm,由匀变速直线运动的规律得△h=gT2,联立可求出初速度v0.再有中间时刻的瞬时速度等于这段时间的平均速度规律求出B点的竖直速度VBy,接着用VBy=VAy+gT和VAy=gt求出从抛出到A点的时间t,这样可求出从抛出到A点的水平位移x=v0t和竖直位移y=
gt2,那么就可以求出小球开始做平抛运动的位置坐标(x,y分别在x轴、y轴的负半轴,应为负值.).
| 1 |
| 2 |
解答:解:从坐标中可看出从A→B→C的水平位移一样,都为△x=10cm,说明各段的时间相等,设为T,可知:
△x=v0T,分析A→B→C的竖直位移依次相差△h=10cm,由匀变速直线运动的规律得:△h=gT2,
联立可求出初速度v0=△x
,代入数值得v0=0.1×
m/s=1.0m/s.
由中间时刻的瞬时速度等于这段时间的平均速度得B的竖直速度:VBy=
=
=
=
×
m/s=2m/s,
又VBy=VAy+gT,∴VAy=VBy-gT=2m/s-10×0.1m/s=1m/s,又VAy=gt,∴从抛出到A点的时间t=
=
s=0.1s,
因此从抛出到a点的水平位移x=v0t=1.0×0.1 m=0.1m=10cm,
竖直位移y=
gt2=
×10×(0.1) 2m=0.05m=5cm,
那么物体开始做平抛运动的位置坐标(-10cm,-5cm).
故答案:1,(-10,-5).
△x=v0T,分析A→B→C的竖直位移依次相差△h=10cm,由匀变速直线运动的规律得:△h=gT2,
联立可求出初速度v0=△x
|
|
由中间时刻的瞬时速度等于这段时间的平均速度得B的竖直速度:VBy=
| hAC |
| 2T |
| hAC | ||||
2
|
| hAC |
| 2 |
|
| 0.4 |
| 2 |
|
又VBy=VAy+gT,∴VAy=VBy-gT=2m/s-10×0.1m/s=1m/s,又VAy=gt,∴从抛出到A点的时间t=
| VAy |
| g |
| 1 |
| 10 |
因此从抛出到a点的水平位移x=v0t=1.0×0.1 m=0.1m=10cm,
竖直位移y=
| 1 |
| 2 |
| 1 |
| 2 |
那么物体开始做平抛运动的位置坐标(-10cm,-5cm).
故答案:1,(-10,-5).
点评:平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动.由坐标分析物体水平方向和竖直方向的运动特点,充分利用匀变速直线运动的规律来求解,所求的坐标为负值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 在研究平抛物体运动的实验中,用一张印有小方格的纸
在研究平抛物体运动的实验中,用一张印有小方格的纸