题目内容
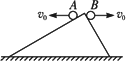
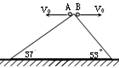
如图所示，两斜面的倾角分别为37°和53°，在顶点把A、B两个相同的小球同时以相同大小的初速度分别向左、右水平抛出，小球都落在斜面上，不计阻力，则先落到斜面上的是A
A
小球，且A、B两小球运动时间之比为9：16
9：16
．（sin37°=0.6，sin53°=0.8）分析：两球都落在斜面上，位移上有限制，即竖直位移与水平位移的比值等于斜面倾角的正切值．
解答：解：对于A球，tan37°=
=
，所以tA=
对于B球，tan53°=
=
，所以tB=
所以
=
=
所以tA＜tB，故A球先落到斜面上．
故答案为：A，9：16．
| y |
| x |
| ||
| v0tA |
| 2v0tan37° |
| g |
对于B球，tan53°=
| y |
| x |
| ||
| v0tB |
| 2v0tan53° |
| g |
所以
| tA |
| tB |
| tan37° |
| tan53° |
| 9 |
| 16 |
所以tA＜tB，故A球先落到斜面上．
故答案为：A，9：16．
点评：解决本题的关键抓住平抛运动落在斜面上竖直方向上的位移和水平方向上的位移是定值．
练习册系列答案
名校课堂系列答案
相关题目
