题目内容
如图所示，水平U形光滑框架，宽度为1m，电阻忽略不计，导体ab质量是0.2kg，电阻是0.1Ω，匀强磁场的磁感应强度B=0.1T，方向垂直框架向上．现用1N的外力F由静止拉动ab杆，当ab的速度达到1m/s时，求此时刻ab 杆产生的感应电动势的大小和它的加速度的大小？分析：（1）根据E=BLv求出感应电动势
（2）求出感应电动势从而求出感应电流，根据F安=BIL求出ab棒所受的安培力．根据牛顿第二定律求出加速度．
（2）求出感应电动势从而求出感应电流，根据F安=BIL求出ab棒所受的安培力．根据牛顿第二定律求出加速度．
解答：解：解：（1）根据导体棒切割磁感线的电动势
E=BLv=0.1v
（2）由闭合电路欧姆定律得回路电流I=
ab所受安培力 F安=BIL=0.1N，
根据牛顿第二定律F-F安=ma
得ab杆的加速度a=
=4.5m/s2．
答：此时刻ab 杆产生的感应电动势的大小0.1v，它的加速度的大小是4.5m/s2．
E=BLv=0.1v
（2）由闭合电路欧姆定律得回路电流I=
| E |
| R |
ab所受安培力 F安=BIL=0.1N，
根据牛顿第二定律F-F安=ma
得ab杆的加速度a=
| F-F安 |
| m |
答：此时刻ab 杆产生的感应电动势的大小0.1v，它的加速度的大小是4.5m/s2．
点评：解决本题的关键掌握导体切割产生的感应电动势E=BLv，以及熟练运用牛顿第二定律．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
如图所示，水平U形光滑固定框架，宽度为L=1m，电阻忽略不计，导体棒ab的质量m=0.2kg、电阻R=0.5Ω，匀强磁场的磁感应强度B=0.2T，方向垂直框架平面向上．现用F=1N的外力由静止开始向右拉ab棒，当ab棒的速度达到5m/s时，求：
如图所示，水平U形光滑框架，宽度L=1m，电阻R=0.4Ω，导体棒ab的质量m=0.5kg，电阻r=0.1Ω，匀强磁场的磁感应强度B=0.4T，方向垂直框架向上，其余电阻不计．现用一水平拉力F由静止开始向右拉ab棒，当ab棒的速度达到2m/s时，求：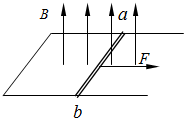
如图所示，水平U形光滑框架，宽度为0.5m，电阻忽略不计，导体ab质量是0.2kg，电阻是0.1Ω，匀强磁场的磁感应强度为0.2T，方向垂直框架向上，现用1N的外力F由静止拉动ab杆，当ab的速度达到1m/s时，求
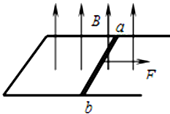如图所示，水平U形光滑固定框架，宽度为L=1m，电阻忽略不计，导体棒ab的质量m=0.2kg、电阻R=0.5Ω，匀强磁场的磁感应强度B=0.2T，方向垂直框架平面向上．现用F=1N的外力由静止开始向右拉ab棒，当ab棒的速度达到5m/s时，求：