题目内容
6. 如图所示,在xoy平面第一象限里有竖直向下的匀强电场,电场强度为E.第二象限里有垂直于纸面向外的匀强磁场,磁感应强度为B.在x轴上-a处,质量为m、电荷量为e的质子以大小不同的速度射入磁场,射入时速度与x轴负方向夹角为α.不计空气阻力,重力加速度为g.求:
如图所示,在xoy平面第一象限里有竖直向下的匀强电场,电场强度为E.第二象限里有垂直于纸面向外的匀强磁场,磁感应强度为B.在x轴上-a处,质量为m、电荷量为e的质子以大小不同的速度射入磁场,射入时速度与x轴负方向夹角为α.不计空气阻力,重力加速度为g.求:(1)在-x轴上有质子到达的坐标范围;
(2)垂直于y轴进入电场的质子,在电场中运动的时间;
(3)在磁场中经过圆心角为2α的一段圆弧后进入电场的质子,到达x轴的动能.
分析 (1)由题意可知,粒子的半径与速度成正比,故半径有无数种可能;根据题意可知,落到O点的第一个点应与y轴相切;根据几何关系可求得粒子所打在的位置,则可明确粒子范围;
(2)粒子在电场中做类平抛运动,由运动的合成与分解可求得时间;
(3)由题意明确粒子在磁场中运动的轨迹,再根据功能关系可求得到达x轴时的动能;
解答  解:(1)设-x轴的第一个坐标点为x1
解:(1)设-x轴的第一个坐标点为x1
当粒子轨迹恰好与y轴相切时,粒子能到达-x轴上;
由几何关系有:
R+Rsinα=a
$R-Rsinα=\overline{O{x_1}}$
解得:$\overline{O{x_1}}=\frac{a(1-sinα)}{1+sinα}$
故坐标范围为:$[-a,\frac{a(1-sinα)}{1+sinα}]$
(2)质子垂直进入电场时距x轴的距离为:H=R+y1
R=asinα
y1=Rcosα
$H=\frac{1}{2}a{t^2}$
$t=\sqrt{\frac{2ma(1+cosα)}{Eesinα}}$
(3)在磁场中运动情景如图所示.$s=\frac{a}{cos(π-2α)}=-\frac{a}{cos2α}$
$R=\frac{{\frac{s}{2}}}{sinα}=-\frac{a}{2sinα•cos2α}$
y=a•tan(π-2α)=-atan(2α)
$Be{υ_0}=m\frac{{{υ_0}^2}}{R}$
$Eey={E_K}-\frac{1}{2}m{υ_0}^2$
${E_K}=-Eeatan(2α)+\frac{{{B^2}{e^2}{a^2}}}{{8m{{sin}^2}α{{cos}^2}(2α)}}$
答:(1)在-x轴上有质子到达的坐标范围$[-a,\frac{a(1-sinα)}{1+sinα}]$;
(2)垂直于y轴进入电场的质子,在电场中运动的时间为$\sqrt{\frac{2ma(1+cosα)}{Eesinα}}$;
(3)在磁场中经过圆心角为2α的一段圆弧后进入电场的质子,到达x轴的动能为-Eeatan(2α)+$\frac{{B}^{2}{e}^{2}{a}^{2}}{8msi{n}^{2}αco{s}^{2}(2α)}$
点评 本题考查带电粒子在电场和磁场中运动,要注意明确在电场中应用类平抛规律求解;而在磁场中应用洛仑兹充当向心力;应用好几何关系进行分析求解即可.

| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | 1:1 |
 如图所示,把一块不带电的锌板接在验电器上,用紫外线灯照射锌板,验电器金属箔张开.下列说法正确的是( )
如图所示,把一块不带电的锌板接在验电器上,用紫外线灯照射锌板,验电器金属箔张开.下列说法正确的是( )| A. | 紫外线是不连续的 | |
| B. | 验电器金属箔带正电 | |
| C. | 从锌板逸出电子的动能都相等 | |
| D. | 改用红外灯照射,验电器金属箔一定张开 |
 在如图所示的电路中,E为电源的电动势,r为电源的内电阻,R1、R2为可变电阻.在下列叙述的操作中,可以使灯泡L的亮度变亮的是( )
在如图所示的电路中,E为电源的电动势,r为电源的内电阻,R1、R2为可变电阻.在下列叙述的操作中,可以使灯泡L的亮度变亮的是( )| A. | 仅使R2的阻值增大 | B. | 仅使R2的阻值减小 | ||
| C. | 仅使R1的阻值增大 | D. | 仅使R1的阻值减小 |
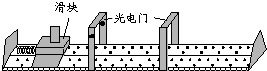 某同学用如图所示装置探究弹簧弹性势能与形变量的关系,弹簧的左端固定在气垫导轨上,遮光片的宽度为d,滑块和遮光板的质量为m.用滑块压缩弹簧,放手后滑块向右运动,用x表示弹簧的压缩量,t表示遮光片通过光电门的时间.
某同学用如图所示装置探究弹簧弹性势能与形变量的关系,弹簧的左端固定在气垫导轨上,遮光片的宽度为d,滑块和遮光板的质量为m.用滑块压缩弹簧,放手后滑块向右运动,用x表示弹簧的压缩量,t表示遮光片通过光电门的时间.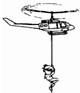 飞机现已广泛应用于突发性灾难的救援工作,如图所示为救助飞行队将一名在海上身受重伤、生命垂危的渔民接到岸上的情景.为了达到最快速的救援效果,飞机一边从静止匀加速收拢缆绳提升伤员,将伤员接进机舱,一边沿着水平方向匀速飞向岸边.则伤员的运动轨迹是( )
飞机现已广泛应用于突发性灾难的救援工作,如图所示为救助飞行队将一名在海上身受重伤、生命垂危的渔民接到岸上的情景.为了达到最快速的救援效果,飞机一边从静止匀加速收拢缆绳提升伤员,将伤员接进机舱,一边沿着水平方向匀速飞向岸边.则伤员的运动轨迹是( )
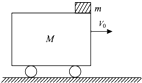 一辆车顶光滑的平板车长L=2m,高h=0.8m,质量M=12kg,在牵引力为零时,仍在向前运动.车与路面的动摩擦因数为0.3,当车速为v0=4m/s时,把一个质量为m=3kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远(结果保留两位小数)?(g=10m/s2 )
一辆车顶光滑的平板车长L=2m,高h=0.8m,质量M=12kg,在牵引力为零时,仍在向前运动.车与路面的动摩擦因数为0.3,当车速为v0=4m/s时,把一个质量为m=3kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远(结果保留两位小数)?(g=10m/s2 ) 如图所示,线圈L与灯泡并联后接到电源上.先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡的电流为I2.现断开开关S,则通过小灯泡的电流方向反向(填“不变”或“反向”);若实验中发现小灯泡闪亮一下再熄灭,则说明I1>I2(填“>”、“<”或“=”).
如图所示,线圈L与灯泡并联后接到电源上.先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡的电流为I2.现断开开关S,则通过小灯泡的电流方向反向(填“不变”或“反向”);若实验中发现小灯泡闪亮一下再熄灭,则说明I1>I2(填“>”、“<”或“=”).