Question

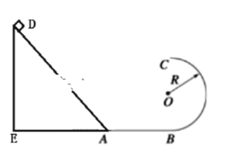
【题目】如图所示，水平面AB与斜面衔接于A点，与竖直面内的半圆形导轨在B点相切，半圆形导轨的半径为R，斜面高DE为4R，EB长为5R．一个质量为m的物体从斜面顶端静止释放，经过A点时无动能损失，当它经过B点进入半圆形导轨的瞬间对轨道的压力为其重力的8倍，之后向上运动恰能到达最高点C，C、O、B三点在同一竖直线上．斜面与水平面的动摩擦因数相同但未知（不计空气阻力），试求：

(1)物体到达B点时的速度大小；

(2)斜面与水平面的动摩擦因数μ；

(3)物体从B点运动至C点的过程中产生的内能．

Answer 1

【答案】(1)(2)0.1(3)mgR

【解析】

(1)设物体在B点的速度为vB，所受的轨道的支持力为FN，物体在B点受到重力和支持力，由牛顿第二定律有：

FN﹣mg=m

据题得

FN=8mg

联立解得

vB=

(2)设EA长为X ，斜面倾角为θ，从D到B摩擦力做的功为

从D到B，由动能定理

得

μ=0.1

(3)设物体在C点的速度为vC，由题意可得：

mg=m

物体由B点运动到C点的过程中，由能量守恒定律得：产生的内能

Q=mvB2﹣(mvC2+2mgR)，

解得：

Q=mgR