题目内容
【题目】如图甲所示,质量m=2 kg的物体置于倾角为θ=53°的固定斜面的底端(斜面足够长),对物体施加平行于斜面向上的拉力F,t1=2 s时拉力大小变为原来的三分之一并反向,t2=3 s时撤去外力,物体运动的部分v-t图象如图乙所示,设物体受到的最大静摩擦力等于滑动摩擦力,取g=10 m/s 2,sin 53°=0.8,求:
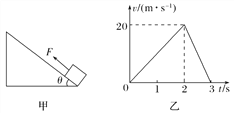
(1)物体与斜面间的动摩擦因数和拉力F的大小;
(2)3 s后再经多长时间物体回到斜面底端。
【答案】(1)0.75;45 N(2)![]() s
s
【解析】试题分析:(1)根据v-t图象的斜率求出匀加速运动和匀减速运动的加速度大小.对两个过程,分别运用牛顿第二定律列式,联立可求得动摩擦因数和拉力F的大小;(2)根据v-t图象的“面积”求得物体上滑的最大距离.撤去外力后,物体下滑过程,运用牛顿第二定律和位移公式结合求解运动时间.
(1)由v-t图线知,物体匀加速运动时加速度大小为![]()
由牛顿第二定律得![]()
物体匀减速运动时加速度大小为![]()
由牛顿第二定律得![]()
联立并代入数据解得![]() 。
。
(2)由v-t图线知物体上滑的总距离为![]()
设撤去外力后物体的加速度大小为![]() ,由牛顿第二定律得
,由牛顿第二定律得![]()
代入数据解得![]()
设3s后再经过间t物体回到斜面底端,由运动学规律知![]()
代入数据解得![]()

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目