Question

如图所示，倒置的光滑圆锥面内侧，有质量相同的两个小玻璃球A、B，沿锥面在水平面内作匀速圆周运动，关于A、B两球的角速度、线速度和向心加速度正确的说法是（　　）

A．它们的角速度相等ω_A=ω_B

B．它们的线速度υ_A＜υ_B

C．它们的向心加速度相等

D．A球的向心加速度大于B球的向心加速度

Answer 1

分析：对两小球分别受力分析，求出合力，根据向心力公式和牛顿第二定律列式求解，可得向心加速度、线速度和角速度．

解答：解：对A、B两球分别受力分析，如图

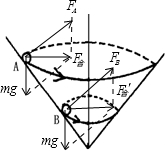
由图可知
 F_合=F_合′=mgtanθ
根据向心力公式有
  mgtanθ=ma=mω²R=m

v2

R

解得
  a=gtanθ
  v=

gRtanθ

ω=

gtanθ R

由于A球转动半径较大，故向心加速度一样大，A球的线速度较大，角速度较小；
故选C．

点评：本题关键受力分析后，求出合力，然后根据向心力公式和牛顿第二定律列式求解．