题目内容
20.有一质量很大而体积很小的星球,一个物体从离这个星球距离为r的高度从静止出发自由落向此星球,则物体落到这个星球上经历的时间为$\frac{1}{2}$$\sqrt{\frac{{π}^{2}{r}^{3}}{2GM}}$(已知星球的质量为M)分析 星球很小,可以看作质点,物体仅受星球引力作用下的运动轨道通常有三种可能的情况:(1)沿直线自由下落.(2)圆轨道.(3)椭圆轨道.物体在椭圆轨道上运动时,星球处于椭圆的一个焦点上,物体的运动规律满足开普勒第三定律:$\frac{{T}^{2}}{{R}^{3}}$=$\frac{4{π}^{2}}{GM}$,其中T为物体的公转周期,R为半长轴,M是星球的质量.我们设想一个狭长的椭圆轨道,远地点即为物体开始下落的位置,此椭圆越扁,其两侧就越向物体自由下落的轨道靠拢,极端的情况是:当椭圆的半短轴b=0时,两者就重合了.这样,就可能通过求物体沿上述椭圆轨道对应部分的时间来求物体自由下落的时间.
解答 解:将星球看成质点,设物体下落的时间为t.则物体绕星球公转的周期为2t,椭圆半长轴为$\frac{r}{2}$,由开普勒第三定律$\frac{{T}^{2}}{{R}^{3}}$=$\frac{4{π}^{2}}{GM}$,得:
$\frac{(2t)^{2}}{(\frac{r}{2})^{2}}$=$\frac{4{π}^{2}}{GM}$
解得:t=$\frac{1}{2}$$\sqrt{\frac{{π}^{2}{r}^{3}}{2GM}}$
故答案为:$\frac{1}{2}$$\sqrt{\frac{{π}^{2}{r}^{3}}{2GM}}$.
点评 本题中物体的加速度不恒定,直接根据运动学规律不好解,关键要运用极限法,建立物体运动的模型:椭圆运动,星球是椭圆的焦点,运用开普勒第三定律$\frac{{T}^{2}}{{R}^{3}}$=$\frac{4{π}^{2}}{GM}$求解.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.关于速度(v)、速度的变化量(△V=V2-V1)、加速度(a=$\frac{△V}{△t}$)的描述正确的是( )
| A. | 速度大,速度的变化量也一定大 | B. | 速度变化量大,加速度一定大 | ||
| C. | 速度大,加速度可能等于零 | D. | 速度大,速度变化量可能等于零 |
11.关于电场,下列说法中错误的是( )
| A. | 电荷的周围存在电场 | |
| B. | 电场对电荷有力的作用 | |
| C. | 由于电场是看不见的,所以电场是虚构的不存在的 | |
| D. | 点电荷周围的电场不是均匀的 |
8. 如图所示,距离水平地面高为h的飞机沿水平方向做匀加速直线运动,从飞机上以相对地面的速度v0依次从a、b、c水平抛出甲、乙、丙三个物体,抛出的时间间隔均为T,三个物体分别落在水平地面上的A、B、C三点,若AB=l1、AC=l2,不计空气阻力,下列说法正确的是( )
如图所示,距离水平地面高为h的飞机沿水平方向做匀加速直线运动,从飞机上以相对地面的速度v0依次从a、b、c水平抛出甲、乙、丙三个物体,抛出的时间间隔均为T,三个物体分别落在水平地面上的A、B、C三点,若AB=l1、AC=l2,不计空气阻力,下列说法正确的是( )
 如图所示,距离水平地面高为h的飞机沿水平方向做匀加速直线运动,从飞机上以相对地面的速度v0依次从a、b、c水平抛出甲、乙、丙三个物体,抛出的时间间隔均为T,三个物体分别落在水平地面上的A、B、C三点,若AB=l1、AC=l2,不计空气阻力,下列说法正确的是( )
如图所示,距离水平地面高为h的飞机沿水平方向做匀加速直线运动,从飞机上以相对地面的速度v0依次从a、b、c水平抛出甲、乙、丙三个物体,抛出的时间间隔均为T,三个物体分别落在水平地面上的A、B、C三点,若AB=l1、AC=l2,不计空气阻力,下列说法正确的是( )| A. | 物体甲在空中运动的时间为t甲<t乙<t丙 | |
| B. | 飞机的加速度为$\frac{{{l_2}-{l_1}}}{T^2}$ | |
| C. | 物体乙刚离开飞机时飞机的速度为$\frac{l_2}{2T}$ | |
| D. | 三个物体在空中运动时总在一条竖直线上 |
15. 质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )
质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )
 质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )
质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的动摩擦因数均为μ,系统在水平拉力F作用下匀速向右运动,选水平向右为正方向,如图所示.如突然撤消拉力F,则刚撤消后瞬间,二者的加速度aA和aB分别为( )| A. | aA=0,aB=0 | B. | aA>0,aB<0 | C. | aA<0,aB>0 | D. | aA<0,aB=0 |
9.下列关于光的现象描述正确的是( )
| A. | 光的衍射现象为光的波动说提供了有力的证据 | |
| B. | 肥皂泡上的彩色条纹是由薄膜干涉所形成的 | |
| C. | 阳光下茂密树荫中地面上的圆形亮斑是由于光的衍射所形成 | |
| D. | 在双缝干涉实验中,把入射光由绿光变成紫光,干涉条纹间距变小 |

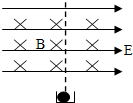 一天然放射性元素放出三种射线,经正交电磁场区域,调整电场强度E和磁感强度B的大小,使α粒子作直线运动,在图中画出β粒子的轨迹.(β粒子的速度接近于光速)
一天然放射性元素放出三种射线,经正交电磁场区域,调整电场强度E和磁感强度B的大小,使α粒子作直线运动,在图中画出β粒子的轨迹.(β粒子的速度接近于光速) “验证力的平行四边形定则”实验的步骤如下,请你将实验步骤补充完整.
“验证力的平行四边形定则”实验的步骤如下,请你将实验步骤补充完整.