Question

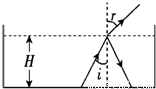
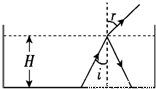
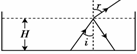
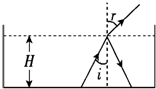一足够大的水池内盛有某种透明液体，液体的深度为H，在水池的底部中央放一点光源，其中一条光线以30°入射角射到液体与空气的界面上，它的反射光线与折射光线的夹角为105°，如图所示．求：
（1）这种液体的折射率；
（2）液体表面亮斑的面积．

Answer 1

分析：（1）由题，已知入射角i=30°，折射角r=45°，根据折射定律求解该液体的折射率；
（2）当光恰好发生全反射，亮斑面积最大，由sinc=

1

n

可求出临界角，再由几何关系，可求出光斑面积．

解答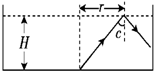：解：（1）由图知：入射角i=30°折射角r=45°
n=

sinr

sini

=

2

（2）若发生全反射，入射角C应满足
由sinc=

1

n

可得：
C=45°
亮斑半：R=Htanc=H
亮斑面积：S=πH²
答：（1）这种液体的折射率

2

；
（2）液体表面亮斑的面积πH²

点评：考查光的折射定律与光的全反射现象，运用几何知识来解题，同时注意全反射的条件．