题目内容
18.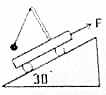 如图所示,在倾角为30°的光滑固定的斜面上放有一质量为M的小车,小车上又用细线悬挂一质量为M的小球.现在小车上作用一平行斜面向上的力F=2Mg,试求系统一起运动时细线对小球的拉力.
如图所示,在倾角为30°的光滑固定的斜面上放有一质量为M的小车,小车上又用细线悬挂一质量为M的小球.现在小车上作用一平行斜面向上的力F=2Mg,试求系统一起运动时细线对小球的拉力.
分析 先对整体进行分析,由牛顿第二定律可求得整体的加速度;再隔离小球进行分析,根据牛顿第二定律可求得合力;再由几何关系可求得绳子的拉力.
解答 解:将小车和小球视为整体,则对整体分析可知,整体受重力、支持力及拉力作用;
由牛顿第二定律可知:
F-2Mgsin30°=2Ma
解得:a=0.5g;
再对小球分析可知,小球受重力和绳子的拉力作用而沿斜面向上做匀加速运动;
拉力与重力的合力沿斜面方向,由几何关系可知,拉力T=$\sqrt{{(Mg)}^{2}+{(M\frac{g}{2})}^{2}-2(Mg)(M\frac{g}{2})cos120°}$=$\frac{\sqrt{7}Mg}{2}$
答:细绳对小球的拉力为$\frac{\sqrt{7}Mg}{2}$
点评 本题考查牛顿第二定律的应用,要注意明确整体法与隔离法的正确应用,同时注意数学规律在解题中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12. 污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )
污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )
 污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )
污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c.左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,测出电极间的电势差U,就可测出污水流量Q(单位时间内流出的污水体积).则( )| A. | 前表面的电势低于后表面的电势 | |
| B. | 若污水为电中性,则两极间的电势差为零 | |
| C. | 若污水中离子浓度越高,则两极间的电势差越大 | |
| D. | 若管道中污水流量越大,则两极间的电势差越大 |
6.做简谐运动的物体在通过平衡位置时,下列物理量中达到最大值的是( )
| A. | 加速度 | B. | 位移 | C. | 回复力 | D. | 动能 |
13.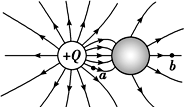 将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )
将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )
 将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )
将一电荷量为+Q的小球放在原来不带电的金属球附近,最终所形成的电场线分布如图所示,a、b为电场中的两点,c、d为金属球表面与内部上两点(未标出),则( )| A. | a点的电场强度比b点的大 | |
| B. | a点的电势比b点的高,而c、d电势不相等 | |
| C. | c点的电势比b点的高,且c、d电势相等 | |
| D. | 将检验电荷-q从a点移到b点的过程中,电场力做负功 |
3. 一个喷水池的池底中央安装了一只射灯,射灯发出的一束光照在右边的池壁上,当池内无水时,站在池旁左边的人,看到在S点形成一个亮斑,如图所示,现往池内灌水,水面升至a位置时,人看到亮斑的位置在P点,如果水面升至b位置时,人看到亮斑的位置在Q点,则( )
一个喷水池的池底中央安装了一只射灯,射灯发出的一束光照在右边的池壁上,当池内无水时,站在池旁左边的人,看到在S点形成一个亮斑,如图所示,现往池内灌水,水面升至a位置时,人看到亮斑的位置在P点,如果水面升至b位置时,人看到亮斑的位置在Q点,则( )
 一个喷水池的池底中央安装了一只射灯,射灯发出的一束光照在右边的池壁上,当池内无水时,站在池旁左边的人,看到在S点形成一个亮斑,如图所示,现往池内灌水,水面升至a位置时,人看到亮斑的位置在P点,如果水面升至b位置时,人看到亮斑的位置在Q点,则( )
一个喷水池的池底中央安装了一只射灯,射灯发出的一束光照在右边的池壁上,当池内无水时,站在池旁左边的人,看到在S点形成一个亮斑,如图所示,现往池内灌水,水面升至a位置时,人看到亮斑的位置在P点,如果水面升至b位置时,人看到亮斑的位置在Q点,则( )| A. | P点在S点的下方,Q点在S点的上方 | B. | P点在S点的上方,Q点在S点的下方 | ||
| C. | P点在S点的上方,Q点在S点的上方 | D. | P点在S点的下方,Q点在S点的下方 |
10. 如图所示,一木块放在粗糙的水平桌面上处于静止状态,其中F1=8N,F2=1N,若撤去F1,则木块受到的摩擦力为( )
如图所示,一木块放在粗糙的水平桌面上处于静止状态,其中F1=8N,F2=1N,若撤去F1,则木块受到的摩擦力为( )
 如图所示,一木块放在粗糙的水平桌面上处于静止状态,其中F1=8N,F2=1N,若撤去F1,则木块受到的摩擦力为( )
如图所示,一木块放在粗糙的水平桌面上处于静止状态,其中F1=8N,F2=1N,若撤去F1,则木块受到的摩擦力为( )| A. | 7N,方向向左 | B. | 7N,方向向右 | C. | 1N,方向向左 | D. | 1N,方向向右 |
7.在如图所示的电路中,U=12V,若电压表的示数也是12V,这说明可能( )


| A. | 灯泡L开路 | B. | 电阻R1、R2中有开路发生 | ||
| C. | 电阻R1、R2中有短路发生 | D. | 灯泡L和电阻R1都发生了开路 |
8. 电冰箱工作时,应当使用图中的乙插座,这是为了使电冰箱的外壳接地,保证安全工作.下表是某电冰箱的部分技术参数,它正常工作时,电压是220V,若压缩机连续正常工作1h,将消耗电量0.2kW•h.
电冰箱工作时,应当使用图中的乙插座,这是为了使电冰箱的外壳接地,保证安全工作.下表是某电冰箱的部分技术参数,它正常工作时,电压是220V,若压缩机连续正常工作1h,将消耗电量0.2kW•h.
 电冰箱工作时,应当使用图中的乙插座,这是为了使电冰箱的外壳接地,保证安全工作.下表是某电冰箱的部分技术参数,它正常工作时,电压是220V,若压缩机连续正常工作1h,将消耗电量0.2kW•h.
电冰箱工作时,应当使用图中的乙插座,这是为了使电冰箱的外壳接地,保证安全工作.下表是某电冰箱的部分技术参数,它正常工作时,电压是220V,若压缩机连续正常工作1h,将消耗电量0.2kW•h.| 额定电压 | 频率 | 额定功率 | 容积 |
| 220v | 50HZ | 200W | 180L |