题目内容
某研究小组在“探究加速度和力、质量的关系”时,利用气垫导轨和光电门进行实验.气垫导轨可以在滑块与导轨之间形成很薄的空气膜,从而极大地减少摩擦力的影响,滑块的运动可以近似看成无摩擦运动.光电门可以准确地记录滑块挡光板通过光电门的时间,从而得到滑块通过光电门的速度,如图1所示.
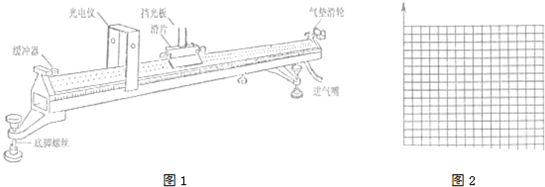
(1)实验时,该小组将托盘和砝码的重力作为滑块所受合外力,但实际上二者只是近似相等,请回答,二者近似相等需耍满足什么条件?
(2)滑块挡光板宽度为么某次实验时发现光电门记录时间为Ah则滑块通过光电门时的速度大小的表达式V= .
(3)该小组保持滑块质量恒定,光电门的位置固定,并且始终从同一位置释放,不断改变砝码的个数,并通过计算得到多组滑块通过光电门的数据,如下表所示.
为了便于研究合外力与加速度的关系,该小组用托盘和砝码的总质量代表合外力作为横轴,请你选择合适的物理量代表加速度作为纵轴,并利用表格中数据在坐标纸中选择标度描点作图.通过绘出的图线2可以得到如下结论:在滑块质量一定时, .

(1)实验时,该小组将托盘和砝码的重力作为滑块所受合外力,但实际上二者只是近似相等,请回答,二者近似相等需耍满足什么条件?
(2)滑块挡光板宽度为么某次实验时发现光电门记录时间为Ah则滑块通过光电门时的速度大小的表达式V=
(3)该小组保持滑块质量恒定,光电门的位置固定,并且始终从同一位置释放,不断改变砝码的个数,并通过计算得到多组滑块通过光电门的数据,如下表所示.
| 托盘砝码总质量(g) | 10 | 20 | 30 | 40 | 50 | 60 |
| V(m/s) | 0.50 | 0.71 | 0.86 | 1.01 | 1.12 | 1.23 |
| l/v(s/m) | 2.00 | 1.41 | 1.16 | 0.99 | 0.89 | 0.81 |
| v2(m2/s2) | 0.25 | 0.50 | 0.74 | 1.02 | 1.25 | 1.51 |
分析:(1)托盘和砝码拖着滑块做加速运动,实际上托盘和砝码的重力和绳子的拉力(滑块的合力)是不等的,根据牛顿第二定律判断在什么条件下可以近似相等
(2)物体在极短时间内的平均速度等于瞬时速度,根据这一结论求出滑块通过光电门时的速度大小的表达式.
(3)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as=
s可知画出v2-m图象可以直观的得出结论.
(2)物体在极短时间内的平均速度等于瞬时速度,根据这一结论求出滑块通过光电门时的速度大小的表达式.
(3)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as=
| 2mg |
| M |
解答:解:(1)设托盘和砝码的质量为m,滑块的质量为M,整体为研究对象根据牛顿第二定律得,a=
绳子的拉力为滑块的合力,根据牛顿第二定律得T=Ma=
=
当m<<M时,托盘和砝码的重力等于滑块所受合外力.
(2)极短时间内的平均速度等于瞬时速度,则滑块通过光电门时的速度大小v=
(3)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as=
s
由题意可知,M、s不变,画出v2-m图象,若图象为过原点的直线,则说明外力和加速度成正比,故画出v2-m图象可以直观的得出结论.
描点作图如图所示:
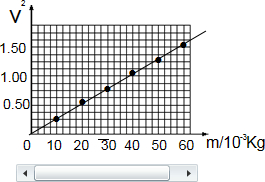
图象是过原点的一条直线,说明在滑块质量一定时,小车的加速度与合外力成正比.
故答案为:(1)托盘和砝码的总质量远小于滑块的质量.(2)v=
(3)
加速度与合外力成正比
| mg |
| m+M |
绳子的拉力为滑块的合力,根据牛顿第二定律得T=Ma=
| Mmg |
| M+m |
| mg | ||
1+
|
当m<<M时,托盘和砝码的重力等于滑块所受合外力.
(2)极短时间内的平均速度等于瞬时速度,则滑块通过光电门时的速度大小v=
| d |
| △t |
(3)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as=
| 2mg |
| M |
由题意可知,M、s不变,画出v2-m图象,若图象为过原点的直线,则说明外力和加速度成正比,故画出v2-m图象可以直观的得出结论.
描点作图如图所示:

图象是过原点的一条直线,说明在滑块质量一定时,小车的加速度与合外力成正比.
故答案为:(1)托盘和砝码的总质量远小于滑块的质量.(2)v=
| d |
| △t |
(3)

加速度与合外力成正比
点评:解决本题的关键知道托盘和砝码的重力等于滑块的合力的条件以及原因,以及掌握极限法的运用.

练习册系列答案
相关题目
 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
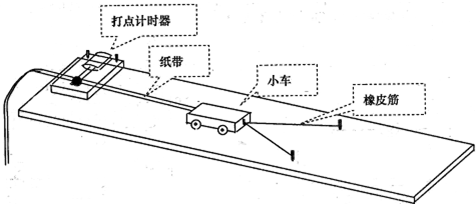
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
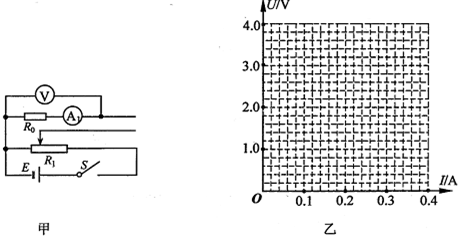
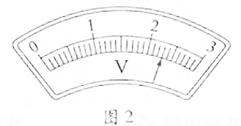
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |

 和
和 的A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影。用小锤打击弹性金属片,使A球沿水平方向飞出,同时松开B球,B球自由下落。A球落到地面N点处,B球落到地面P点处。测得
的A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影。用小锤打击弹性金属片,使A球沿水平方向飞出,同时松开B球,B球自由下落。A球落到地面N点处,B球落到地面P点处。测得 )
)
 ;
; ;
; ;
; ,阻值
,阻值 ;
; ,阻值
,阻值 ;
; ,阻值范围
,阻值范围 ;
; 。
。



 的公式为
的公式为

 和
和 的A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影。用小锤打击弹性金属片,使A球沿水平方向飞出,同时松开B球,B球自由下落。A球落到地面N点处,B球落到地面P点处。测得
的A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影。用小锤打击弹性金属片,使A球沿水平方向飞出,同时松开B球,B球自由下落。A球落到地面N点处,B球落到地面P点处。测得 )
)
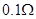 ;
; ;
; ;
; ,阻值
,阻值 ;
; ,阻值
,阻值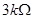 ;
; ,阻值范围
,阻值范围 ;
; 。
。

