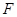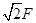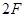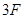Question

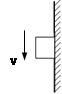
（22分）如图所示，一个长为L的绝缘板固定在水平面上．整个空间有一个水平的匀强电场．板的右半部分有一个垂直于纸面向外的匀强磁场．一质量为m，带电量为q的小物体（视为质点），在电场力的作用下，从板的左端P处由静止开始向右运动。小物体与绝缘板间的动摩擦因数为μ。进入磁场区域后小物体恰好做匀速运动．在小物体碰到绝缘板右端的挡板Q后被弹回．若在碰撞瞬间撤去电场，物体返回过程在磁场中仍能做匀速运动，离开磁场后则做匀减速运动，并停在C点，已知PC=L/4。

求：⑴ 小物体与挡板碰撞前后的速率v₁和v₂；
⑵ 磁感应强度B的大小；
⑶ 电场强度E的大小和方向。

Answer 1

⑴  ⑵ ⑶   向右

试题分析：物体碰挡板后在磁场中做匀速运动，可判断物体带的是正电荷，电场方向向右。
⑴ 物体进入磁场前，在水平方向上受到电场力和摩擦力的作用，由静止匀加速至V₁。
由动能定理得：      ①
物体进入磁场后，做匀速直线运动，电场力与摩擦力相等
      ②
在碰撞的瞬间，电场撤去，此后物体仍做匀速直线运动，速度为V₂，不再受摩擦力，在竖直方向上磁场力与重力平衡。
      ③
离开磁场后，物体在摩擦力的作用下做匀减速直线运动
由动能定理：      ④
由④式可得：
解以上各方程可得：
⑵ 由③式得：
⑶ 由②式可得：
   电场方向向右。