题目内容
(满分12分)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻 ,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
(1)金属棒运动过程中,流过棒的电流多大?方向如何?
(2)金属棒经过多长时间落到地面?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(1)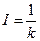 ,方向水平向右
,方向水平向右
(2)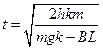
(3)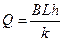
解析(1)(4分)在棒运动过程中,流过电阻R的电流大小为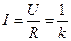 ; ① (2分)
; ① (2分)
电流方向水平向右(从a→b)。 (1分)
(2)(6分)在运动过程中金属棒受到的安培力为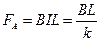
对金属棒运用牛顿第二定律, ③ (1分)
③ (1分)
得 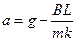 恒定,金属棒作匀加速直线运动;(2分)
恒定,金属棒作匀加速直线运动;(2分)
设金属棒经过时间t落地,有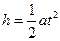 ④
④
解得: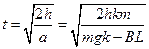 ⑤ (2分)
⑤ (2分)
(3)(4分)设金属棒落地时速度大小为v,有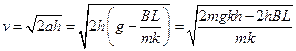 (2分)
(2分)
根据动能定理,有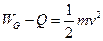
 ⑥
⑥
得 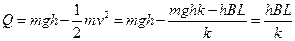 (2分)
(2分)
另解:金属棒从释放到落地过程中在电子元件上消耗的电能等于克服安培力所做的功,即 ⑦ (4分)
⑦ (4分)

练习册系列答案
相关题目
 (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
 ,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问:
,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与光滑框架接触良好,离地高为h,磁感应强度为B的匀强磁场与框架平面垂直。将金属棒由静止释放,棒沿框架向下运动。其它电阻不计,问: (3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?
(3)金属棒从释放到落地过程中在电子元件上消耗的电能多大?