题目内容
A、B两小球在光滑水平面上沿同一直线向同一方向运动,A球的动量为5kg·m/s,B球的动量为7kg·m/s,当A球追上B球时发生对心碰撞,则碰撞后A、B两球动量的可能值为 ( )
| A.pA′=6kg·m/s,pB′=6kg·m/s | B.pA′=3kg·m/s,pB′=9kg·m/s |
| C.pA′=-2kg·m/s,pB′=14kg·m/s | D.pA′=-5kg·m/s,pB′=17kg·m/s |
BC
解析试题分析:由题,碰撞后,两球的动量方向都与原来方向相同,A的动量不可能沿原方向增大.故A错误.碰撞前,A的速度大于B的速度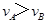 ,则有
,则有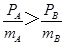 ,得到
,得到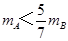 .根据碰撞过程总动能不增加,则有
.根据碰撞过程总动能不增加,则有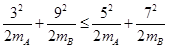 ,得到
,得到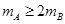 ,满足
,满足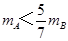 .故B正确.同理C正确;可以看出,碰撞后A的动能不变,而B的动能增大,违反了能量守恒定律.故D错误.
.故B正确.同理C正确;可以看出,碰撞后A的动能不变,而B的动能增大,违反了能量守恒定律.故D错误.
故选BC
考点:动量守恒定律.
点评:对于碰撞过程要遵守三大规律:1、是动量守恒定律;2、总动能不增加;3、符合物体的实际运动情况.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
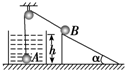 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,B球放在倾角为α的固定光滑斜面上,A球放在装有水的容器底部(容器底部直径足够大).现用手控制住B球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A球的质量为m,重力加速度为g,细线与滑轮之间的摩擦不计,图示状态水的深度为h,A球的体积为V,开始时整个系统处于静止状态.释放B球后,B球沿斜面下滑至速度最大时A球恰好离开水面一半,不计大气压强.下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,B球放在倾角为α的固定光滑斜面上,A球放在装有水的容器底部(容器底部直径足够大).现用手控制住B球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A球的质量为m,重力加速度为g,细线与滑轮之间的摩擦不计,图示状态水的深度为h,A球的体积为V,开始时整个系统处于静止状态.释放B球后,B球沿斜面下滑至速度最大时A球恰好离开水面一半,不计大气压强.下列说法正确的是( )| A、B球沿斜面下滑至速度最大的过程中,B球的机械能增加 | B、从释放B球到A球刚离开水面一半的过程中,A、B两小球组成的系统机械能守恒 | C、在A球再次落到容器底前,A、B两小球和水组成的系统机械能守恒 | D、根据上述条件可以求出B球的质量 |
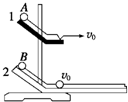
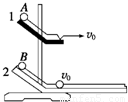
 如图所示,将两个质量相等的小钢球从同一竖直面内的斜面的同一高度处由静止同时释放,滑道2与足够长的光滑水平板相切,则将观察到的现象是A、B两个小球在水平板上
如图所示,将两个质量相等的小钢球从同一竖直面内的斜面的同一高度处由静止同时释放,滑道2与足够长的光滑水平板相切,则将观察到的现象是A、B两个小球在水平板上