题目内容
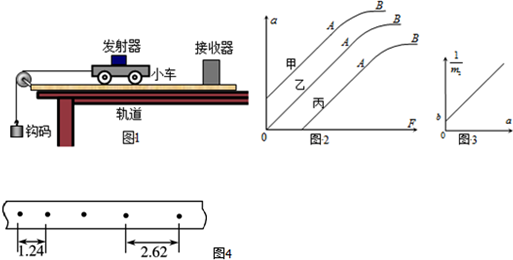
3. 如图所示,两个啮合齿轮,小齿轮半径为R.大齿轮半径为2R.大齿轮中C点离圆心O2的距离为R.A、B分别为两个齿轮边缘上的点,则A、B两点的角速度之比为ωA:ωB=2:1.B、C两点的线速度之比为vB:vC=2:1.A、C两点的向心加速度之比为aA:aC=4:1.
如图所示,两个啮合齿轮,小齿轮半径为R.大齿轮半径为2R.大齿轮中C点离圆心O2的距离为R.A、B分别为两个齿轮边缘上的点,则A、B两点的角速度之比为ωA:ωB=2:1.B、C两点的线速度之比为vB:vC=2:1.A、C两点的向心加速度之比为aA:aC=4:1.
分析 两个啮合齿轮,转动地过程中两个轮子边缘上各点线速度大小相等,同轴传动的各点角速度相等;然后结合v=ωr、a=$r{ω}^{2}=\frac{{v}^{2}}{r}$分析.
解答 解:A、B两点的线速度大小相等,半径之比为1:2,则ωA:ωB=rB:rA=2:1.
B、C的角速度相等,则vB:vC=rB:rC=2:1,
A、B的线速度大小相等,根据a=$\frac{{v}^{2}}{r}$知,aA:aB=rB:rA=2:1,B、C角速度相等,根据a=rω2知,aB:aC=rB:rC=2:1,则A、C的向心加速度之比为4:1.
故答案为:2:1;2:1;4:1
点评 本题关键明确同缘传动时线速度大小相等、同轴传动时角速度相等,结合这些特点,由圆周运动的公式分析解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知某人造地球卫星绕地球公转的半径为r,公转周期为T,万有引力常数为G,则由此可求出( )
| A. | 人造地球卫星的质量 | B. | 地球的密度 | ||
| C. | 第一宇宙速度 | D. | 人造地球卫星运行的角速度 |
14.“小小竹排江中游,巍巍青山两岸走”中,“巍巍群山两岸走”选取的参照物是( )
| A. | 江中竹排 | B. | 两岸青山 | C. | 天上浮云 | D. | 空中飞鸟 |
8.一弹簧振子在一条直线上做简谐运动,第一次先后经过M、N两点时速度v(v≠0)相同,那么,下列说法正确的是( )
| A. | 振子在M、N两点受回复力大小相同 | |
| B. | 振子在M、N两点对平衡位置的位移相同 | |
| C. | 振子在M、N两点加速度大小相等 | |
| D. | 从M点到N点,振子先做匀加速运动,后做匀减速运动 |
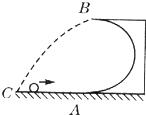 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,A、B分别是半圆形轨道的最低点和最高点一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则:
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,A、B分别是半圆形轨道的最低点和最高点一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则:
 如图所示,质量为1kg的小球用长为0.5m的细线悬挂在O点,O点距地面高度为5.4m.如果使小球绕OO′轴在水平面内做圆周运动,若细线受到拉力为12.5N时就会拉断,求:
如图所示,质量为1kg的小球用长为0.5m的细线悬挂在O点,O点距地面高度为5.4m.如果使小球绕OO′轴在水平面内做圆周运动,若细线受到拉力为12.5N时就会拉断,求: