Question

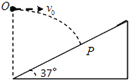
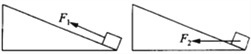
【题目】在如图所示的装置中，表面粗糙的斜面固定在地面上。斜面的倾角为θ＝30°；两个光滑的定滑轮的半径很小，用一根跨过定滑轮的细线连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体悬在空中，并使悬线拉直且偏离竖直方向α＝60°。现同时释放甲、乙两物体，乙物体将在竖直平面内摆动，当乙物体运动经过最高点和最低点时，甲物体在斜面上均恰好未滑动。已知乙物体的质量为m＝1kg，若重力加速度g取10m/s2，下列说法正确的是（ ）

A. 乙物体运动经过最高点时悬线的拉力大小为15N

B. 乙物体运动经过最低点时悬线的拉力大小为25N

C. 斜面对甲物体的最大静摩擦力的大小为l5N

D. 甲物体的质量为2．5kg

Answer 1

【答案】D

【解析】试题分析：乙物体摆到最高点时绳子拉力最小，有：T1＝mgcos60°＝10×N＝5N，故A错误．由最高点到最低点，根据动能定理得：mgl（1cos60°）＝mv2，根据牛顿第二定律得：，联立两式得，T2=20N，故B错误．对甲物体有：m甲gsin30°=T1+fm，m甲gsin30°+fm=T2，联立两式得，m甲=2．5kg，fm=7．5N．故C错误，D正确．故选D。